CF1578G Game of Chance

国王想为他的女儿招婿，他希望女婿拥有尽可能高的天生幸运值。为此，他决定举办一场“抛硬币”锦标赛。 如果幸运值为 $x$ 的选手 $A$ 与幸运值为 $y$ 的选手 $B$ 进行抛硬币比赛，则 $A$ 获胜的概率为 $x/(x+y)$。 锦标赛分为若干轮。每一轮，一些参赛者被分成若干对，每对进行比赛，失败者被淘汰。 参赛者编号为 $1$ 到 $n$。在第一轮时，选择一个 $k$（$1 \le k \le n$），使得 $n-k/2$ 是 $2$ 的幂（这样的 $k$ 总是存在且唯一）。只有编号 $1$ 到 $k$ 的选手参加第一轮。这确保了之后每一轮的参赛人数都是 $2$ 的幂。 在之后的每一轮，所有未被淘汰的选手都参加。如果某一轮有编号为 $p_1 < \ldots < p_{2m}$ 的选手参加，则他们被如下方式分组：对于每个 $i$ 从 $1$ 到 $m$，选手 $p_{2i-1}$ 与选手 $p_{2i}$ 组成一对进行比赛。 比赛一直进行到只剩下一名选手，他将成为锦标赛的冠军，并娶国王的女儿。公主迫不及待地想知道她未来的丈夫是谁。她询问了每位选手的幸运值。假设他们都没有撒谎，她想知道每位选手赢得锦标赛的概率。作为公主最好的朋友，你需要帮助她解决这个问题。

输入的第一行包含参赛人数 $n$（$2 \le n \le 3 \cdot 10^5$）。 第二行包含 $n$ 个整数 $a_1, \ldots, a_n$（$1 \le a_i \le 10^9$），其中 $a_i$ 表示第 $i$ 位选手的幸运值。

输出 $n$ 个数 $p_i$，第 $i$ 个数表示第 $i$ 位选手赢得锦标赛的概率。你的答案的绝对误差不能超过 $10^{-9}$。

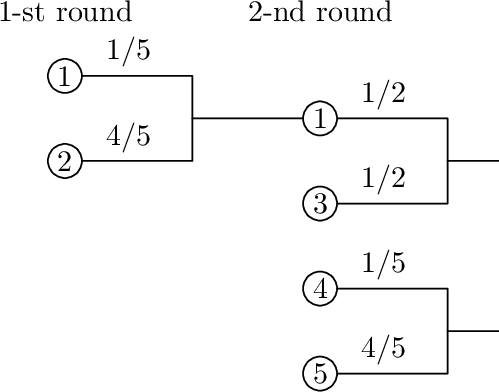
以下是一个锦标赛对阵示例，展示了每一对的获胜概率。  由 ChatGPT 4.1 翻译