CF1578I Interactive Rays

This is an interactive problem. Your goal is to find a circle on a plane by shooting rays and getting the distance to the circle as a result. Interactor has three hidden integer parameters that are determined in advance for each test, but which you don't know — $ x_c $ , $ y_c $ , and $ r_c $ . $ (x_c, y_c) $ are coordinates of the circle's center and $ r_c $ is its radius. The absolute values of $ x_c $ , $ y_c $ , and $ r_c $ do not exceed $ 10^5 $ , and $ 1 \leq r_c \leq \sqrt{x_c^2 + y_c^2} - 1 $ . You can shoot rays that extend from the origin $ (0,0) $ and go via a point $ (x_q,y_q) $ with the integer coordinates you specify. For each ray, you get a distance from the ray to the circle or $ 0 $ if the ray intersects the circle.

N/A

The interaction starts with your program printing a query to the standard output and finishes when your program finds and prints the answer to the problem. Each query has a form of "? $ x_q $ $ y_q $ ", where $ x_q $ and $ y_q $ are integers ( $ |x_q|, |y_q| \le 10^6 $ ; $ x_q \ne 0 $ or $ y_q \ne 0 $ ). The interactor outputs a line with a single floating-point number — the distance between a query ray and a circle that is precise to $ 10^{-10} $ by an absolute value. Your program can make the next query, read the output, and so on. You are allowed to do at most $ 60 $ queries. At the end of the interaction, print the answer line "! $ x_c $ $ y_c $ $ r_c $ ", flush the output and exit. Note, that the output of the interactor is actually rounded to the 10-th digit after a decimal point, so if you are stress-testing your solution locally, make sure that you also perform the corresponding rounding.

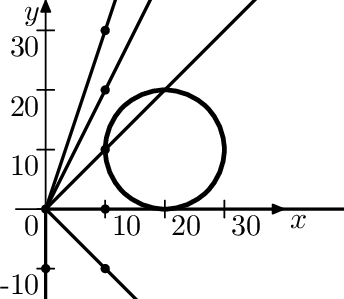Illustration of the queries from the example interaction.