CF1579C Ticks

Casimir 有一张大小为 $n \times m$ 的长方形纸，上面有一个格子状的区域。最初，所有格子都是白色的。 我们用 $i$ 表示纵坐标，$j$ 表示横坐标，将坐标为 $(i, j)$ 的格子称为第 $i$ 行第 $j$ 列的格子。左上角的格子为 $(1, 1)$，右下角的格子为 $(n, m)$。 Casimir 会在纸上画出不同大小的“对勾”。一个大小为 $d$（$d > 0$）且中心在 $(i, j)$ 的对勾的绘制方式如下： 1. 首先，将中心格子 $(i, j)$ 涂黑。 2. 然后，将中心格子左上对角线方向正好 $d$ 个格子和右上对角线方向正好 $d$ 个格子也涂黑。 3. 也就是说，所有满足 $0 \leq h \leq d$ 的格子 $(i-h, j\pm h)$ 都会被涂黑。特别地，一个对勾一共包含 $2d+1$ 个黑色格子。 已经被涂黑的格子如果再次被涂黑，仍然保持黑色。下图是一个 $4 \times 9$ 的格子区域，画了两个大小分别为 $2$ 和 $3$ 的对勾。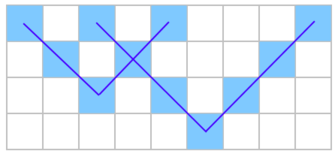  现在给你一个大小为 $n \times m$ 的格子区域的描述。Casimir 声称这个区域是他画了一些（可能为 $0$ 个）对勾后得到的。每个对勾的大小至少为 $k$（即 $d \geq k$）。 请你判断，是否真的可以通过画一些（可能没有）大小不小于 $k$ 的对勾得到这个区域。

第一行包含一个整数 $t$（$1 \leq t \leq 100$），表示测试用例的数量。 接下来是每个测试用例的描述。 每个测试用例的第一行包含三个整数 $n$、$m$ 和 $k$（$1 \leq k \leq n \leq 10$，$1 \leq m \leq 19$），表示区域的大小和对勾的最小大小。接下来的 $n$ 行，每行包含 $m$ 个字符，若对应格子未被涂黑则为 '.'，否则为 '*'。

输出 $t$ 行，每行对应一个测试用例的答案。如果该区域可以通过画一些大小不小于 $k$ 的对勾得到，输出 YES，否则输出 NO。 你可以用任意大小写输出答案（例如 yEs、yes、Yes、YES 都会被识别为正确答案）。

第一个样例测试用例包含两个星号，但它们都不能是独立的对勾，因为不存在大小为 $0$ 的对勾。 第二个样例测试用例已在题面中描述（见题面图片）。该区域可以通过画大小为 $2$ 和 $3$ 的对勾得到，如图所示。 第三个样例测试用例对应于三个大小为 $1$ 的对勾。它们的中心格子分别用 $\color{blue}{\text{蓝色}}$、$\color{red}{\text{红色}}$ 和 $\color{green}{\text{绿色}}$ 标记： \*.\*.\* $\color{blue}{\textbf{*}}$ \*\*. $\color{green}{\textbf{*}}\color{red}{\textbf{*}}$ ..... 第四个样例测试用例可以通过画两个大小分别为 $1$ 和 $2$ 的对勾得到。它们的顶点分别用 $\color{blue}{\text{蓝色}}$ 和 $\color{red}{\text{红色}}$ 标记： .....\*...\*.\*.\*... $\color{red}{\textbf{*}}$ .\*... $\color{blue}{\textbf{*}}$ . 第五个样例测试用例无法得到，因为 $k=2$，而第四行从上数第 $5$ 个星号 $(4, 5)$ 只能属于一个大小为 $1$ 的对勾。 第六个样例测试用例无法得到，因为左上角的星号 $(1, 1)$ 不能是独立的对勾，因为对勾的大小必须为正数，也不能属于以最后一行为中心的对勾，因为它与 $(2, 2)$ 的点（'.'）之间有空隙。 第七个样例测试用例同理，无法通过上述过程得到，因为坐标为 $(1, 2)$（第一行第二个格子）、$(3, 1)$ 和 $(3, 3)$（第三行最左和最右的格子）的星号都不能属于任何对勾。 由 ChatGPT 4.1 翻译