CF1583E Moment of Bloom

她竭尽全力完美地执行人们的最后仪式，并维护世间阴阳的平衡。 胡桃，这位喜欢恶作剧的小家伙，试图用这道图论问题吓唬你！给定一个包含 $n$ 个节点的连通无向图，包含 $m$ 条边。此外还有 $q$ 个查询。每个查询由两个节点 $a$ 和 $b$ 组成。 初始时，图中所有边的权重均为 $0$。对于每个查询，你必须选择一条从 $a$ 开始到 $b$ 结束的简单路径，然后将这条路径上的每条边的权重加 $1$。请判断在处理完所有 $q$ 个查询后，是否可能让图中所有边的权重均为偶数。如果可能，请输出每个查询选择的路径。 如果不可能，请确定需要添加的最少额外查询数量，使得最终可能满足条件。可以证明在给定约束下，这个数值不会超过 $10^{18}$。 简单路径定义为不重复经过任何节点的路径。 边的权重为偶数当且仅当其值能被 $2$ 整除。

第一行包含两个整数 $n$ 和 $m$（$2 \leq n \leq 3 \cdot 10^5$，$n-1 \leq m \leq \min{\left(\frac{n(n-1)}{2}, 3 \cdot 10^5\right)}$）。 接下来的 $m$ 行，每行包含两个整数 $x$ 和 $y$（$1 \leq x, y \leq n$，$x \neq y$），表示节点 $x$ 和 $y$ 之间有一条无向边。输入保证没有自环或重边，且给定的图是连通的。 接下来一行包含一个整数 $q$（$1 \leq q \leq 3 \cdot 10^5$）。 接下来的 $q$ 行，每行包含两个整数 $a$ 和 $b$（$1 \leq a, b \leq n$，$a \neq b$），表示每个查询的描述。 保证 $nq \leq 3 \cdot 10^5$。

如果可以让所有边的权重均为偶数，第一行输出 "YES"，随后输出 $2q$ 行，按顺序描述每个查询选择的路径。对于每个查询，第一行输出一个整数 $x$，表示路径中的节点数量。第二行输出 $x$ 个空格分隔的整数 $p_i$，表示路径（需满足 $p_1 = a$，$p_x = b$，所有数字在 $1$ 到 $n$ 之间）。路径不能包含重复节点且必须是图中的有效简单路径。 如果不可能，第一行输出 "NO"，第二行输出需要添加的最少额外查询数量。

以下是第一个测试用例的查询示意图（红色对应第一个查询，蓝色对应第二个查询，绿色对应第三个查询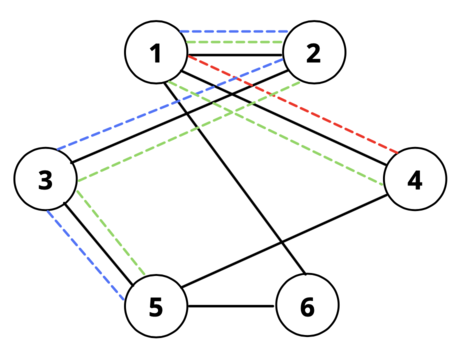）：  注意图中每条边要么未被任何查询覆盖，要么被恰好两个查询覆盖。第二个测试用例的图如下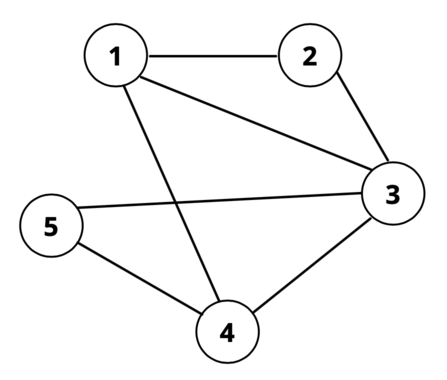：  在给定查询下，无法通过路径选择使所有边的权重均为偶数。至少需要添加 $2$ 个新查询才能满足条件。 翻译由 DeepSeek R1 完成