CF1583F Defender of Childhood Dreams

即使你什么都不做，它们也会自行崩溃。所以，总得有人来保护它们，对吧？ 你又一次在璃月城和托克玩耍。当你带着这个古灵精怪的小孩四处转悠时，你注意到了城市结构中的一些有趣之处。 璃月可以被表示为一个包含 $n$ 个点的有向图。节点编号为 $1$ 到 $n$。当且仅当 $a < b$ 时，存在一条从节点 $a$ 指向节点 $b$ 的有向边。 节点 $a$ 到节点 $b$ 之间的一条路径被定义为一系列有向边，使得你可以从 $a$ 出发，沿着这些边的方向依次前进，最终到达 $b$。路径的长度定义为边的数量。长度为 $x$ 的彩虹路径被定义为：在该路径的 $x$ 条边中，至少存在两种不同的颜色。 托克最喜欢的数字是 $k$。你对以下情景感到好奇：如果你要给每条边染色，最少需要多少种颜色，才能保证所有长度为 $k$ 或更长的路径都是彩虹路径？ 托克想用一张璃月的地图给他哥哥一个惊喜。他还想知道一种使用最少颜色的有效染色方案。请帮助他完成这个任务！

输入仅一行，包含两个整数 $n$ 和 $k$（$2 \leq k < n \leq 1000$）。

第一行输出 $c$，即满足上述要求所需的最少颜色数。 第二行输出一个长度为 $\frac{n(n-1)}{2}$ 的数组，表示每条边的颜色，颜色编号为 $1$ 到 $c$。构造中必须恰好使用 $c$ 种不同的颜色。输出顺序为：先按起点编号升序，再按终点编号升序。 例如，当 $n=4$ 时，边的顺序为：(1,2), (1,3), (1,4), (2,3), (2,4), (3,4)。

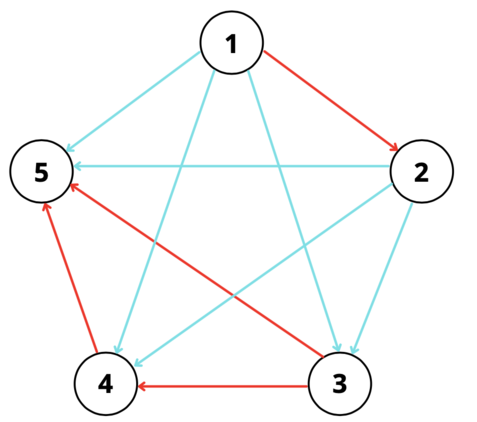
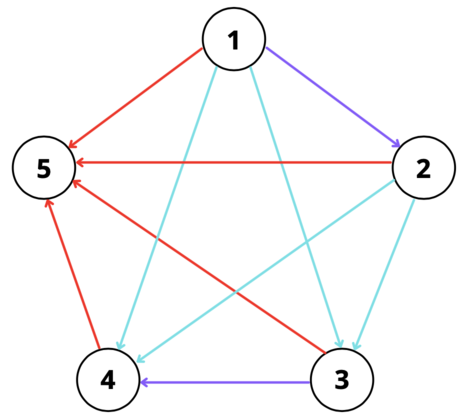
第一个测试点的对应构造如下：  使用少于 $2$ 种颜色无法满足要求。 第二个测试点的对应构造如下：  可以证明，无法使用少于 $3$ 种颜色完成构造。 由 ChatGPT 4.1 翻译