CF1583H Omkar and Tours

Omkar 正在组织他的国家 Omkarland 的旅游团！Omkarland 有 $n$ 个城市，奇特的是，这些城市之间恰好有 $n-1$ 条双向道路相连。保证任意两个城市之间都可以通过道路网络互相到达。 每个城市都有一个欢乐值 $e$。每条道路都有一个容量 $c$，表示该道路上最多可以同时通过的车辆数，以及一个通行费 $t$。然而，Omkarland 的收费系统有一个有趣的特点：如果一辆车在一次旅途中经过了多条道路，他们只需支付所经过道路中通行费最高的那一条的费用（即支付所有经过道路的 $t$ 的最大值）。如果车辆没有经过任何道路，则无需支付通行费。 Omkar 决定组织 $q$ 个旅游团。每个旅游团由 $v$ 辆车组成，起点为城市 $x$。（请注意，只有容量 $\geq v$ 的道路才能被该旅游团通过。）作为组织者，Omkar 希望他的团队能尽可能多地享受乐趣，但同时也必须为他们报销通行费。因此，对于每个旅游团，Omkar 想知道两件事：首先，该旅游团从起点城市出发，能够到达的城市中欢乐值最大的城市的欢乐值是多少；其次，Omkar 需要为整个团队报销的每辆车的通行费是多少？（从 $x$ 到 $y$ 的行程总是选择最短路径。） 如果有多个可达城市的欢乐值相同且最大，Omkar 会让旅游团自行选择。因此，为了应对所有可能的情况，他需要知道无论团队选择哪个城市，自己都需要为团队报销的最大金额。

第一行包含两个整数 $n$ 和 $q$（$2 \leq n \leq 2 \cdot 10^5$，$1 \leq q \leq 2 \cdot 10^5$），分别表示城市数量和旅游团数量。 第二行包含 $n$ 个整数 $e_1, e_2, \ldots, e_n$（$1 \leq e_i \leq 10^9$），其中 $e_i$ 表示第 $i$ 个城市的欢乐值。 接下来的 $n-1$ 行，每行包含四个整数 $a$、$b$、$c$ 和 $t$（$1 \leq a,b \leq n$，$1 \leq c \leq 10^9$，$1 \leq t \leq 10^9$），表示城市 $a$ 和城市 $b$ 之间有一条容量为 $c$、通行费为 $t$ 的道路。 接下来的 $q$ 行，每行包含两个整数 $v$ 和 $x$（$1 \leq v \leq 10^9$，$1 \leq x \leq n$），表示旅游团的车辆数和起点城市编号。

输出 $q$ 行。第 $i$ 行输出两个整数：该旅游团能够到达的城市中最大欢乐值，以及 Omkar 需要为该旅游团每辆车报销的最大通行费。

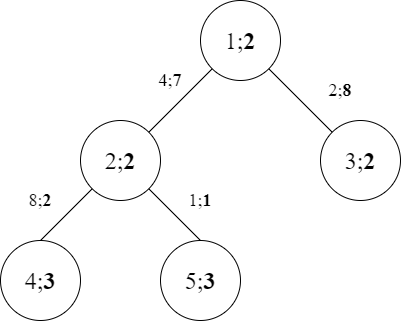
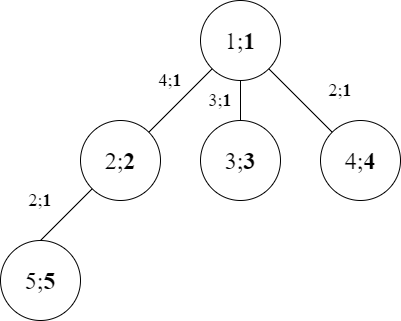
下图为第一个样例的地图。节点中未加粗的数字为编号，加粗的数字为欢乐值。边上的未加粗数字为容量，加粗数字为通行费。  对于第一个询问，1 辆车从城市 3 出发，可以到达城市 1、2、3、4、5。最大欢乐值为 3。如果团队选择去城市 4，Omkar 需要为每辆车报销 8 元通行费，这是最大值。 对于第二个询问，9 辆车从城市 5 出发，只能到达城市 5。最大欢乐值仍为 3，Omkar 需要报销 0 元。 对于第三个询问，6 辆车从城市 2 出发，可以到达城市 2 和 4。最大欢乐值为 3。如果团队选择去城市 4，Omkar 需要为每辆车报销 2 元通行费，这是最大值。 下图为第二个样例的地图：  对于第一个询问，5 辆车从城市 1 出发，只能到达城市 1。最大欢乐值为 1，Omkar 需要报销 0 元。 对于第二个询问，4 辆车从城市 1 出发，可以到达城市 1 和 2。最大欢乐值为 2，Omkar 需要报销 1 元。 对于第三个询问，3 辆车从城市 1 出发，可以到达城市 1、2、3。最大欢乐值为 3，Omkar 需要报销 1 元。 对于第四个询问，2 辆车从城市 1 出发，可以到达城市 1、2、3、4。最大欢乐值为 4，Omkar 需要报销 1 元。 对于第五个询问，1 辆车从城市 1 出发，可以到达城市 1、2、3、4、5。最大欢乐值为 5，Omkar 需要报销 1 元。 由 ChatGPT 4.1 翻译