CF1585G Poachers

Alice 和 Bob 是两名在森林中砍树的偷猎者。 森林是由零棵或多棵树组成的集合。一棵树是一个无环连通图。根树有一个特殊的顶点称为根。节点 $v$ 的父节点是从 $v$ 到根的最短路径上的下一个顶点。顶点 $v$ 的子节点是所有以 $v$ 为父节点的节点。如果一个顶点没有子节点，则称其为叶子节点。 在本题中，我们定义顶点的深度为从该顶点到根的简单路径上经过的顶点数。树的秩定义为其所有叶子节点中最小的深度。 初始时有一片由若干根树组成的森林。Alice 和 Bob 在这片森林上玩游戏。两人轮流行动，Alice 先手。每次轮到某位玩家时，他选择森林中的一棵树，然后选择一个正的切割深度（不得超过所选树的秩）。接着，该玩家移除该树中所有深度小于等于切割深度的顶点。剩下的顶点会形成若干棵新的根树，每棵树的根是切割前深度最小的顶点。所有这些新树会加入到游戏森林中，游戏继续进行。 如果在某位玩家行动时森林为空，则该玩家输掉游戏。 请你判断，如果双方都采取最优策略，Alice 是否能赢得游戏。

每组测试数据包含多个测试用例。第一行包含一个整数 $t$（$1 \leq t \leq 5 \cdot 10^5$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$1 \leq n \leq 5 \cdot 10^5$），表示初始森林中顶点的总数。 第二行包含 $n$ 个整数 $p_1, p_2, \ldots, p_n$（$0 \leq p_i \leq n$），表示森林的结构。如果 $p_i = 0$，则第 $i$ 个顶点是某棵树的根，否则 $p_i$ 是第 $i$ 个顶点的父节点。保证 $p$ 描述的是一个合法的根树森林。 保证所有测试用例中 $n$ 的总和不超过 $5 \cdot 10^5$。

对于每个测试用例，如果 Alice 能获胜，输出 "YES"（不含引号），否则输出 "NO"（不含引号）。你可以使用大写或小写字母。

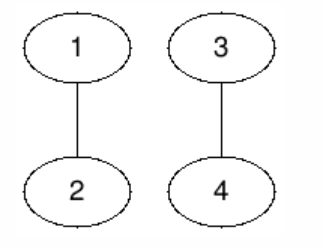
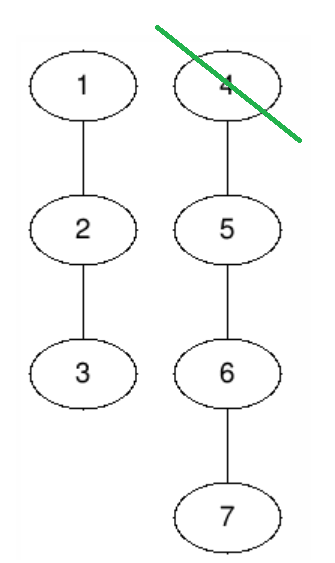
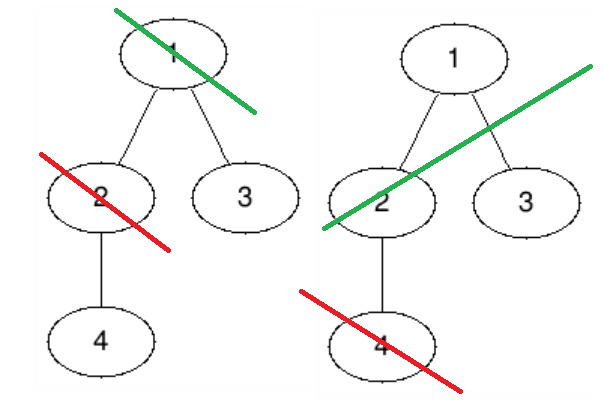
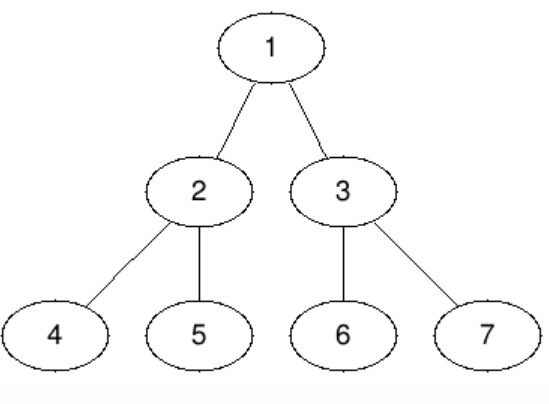
在第一个测试用例中，Bob 有对称策略，因此 Alice 无法获胜。  在第二个测试用例中，Alice 可以选择第二棵树并选择切割深度 $1$，从而得到一个她可以采取对称策略的森林。  在第三个测试用例中，唯一一棵树的秩为 $2$，Alice 的两种可能操作都会导致失败。Bob 可以让自己获得对称森林，或者直接清空森林。  在第四个测试用例中，所有叶子节点深度相同，因此 Alice 可以一步清空森林。  由 ChatGPT 4.1 翻译