CF1588F Jumping Through the Array

You are given an array of integers $ a $ of size $ n $ and a permutation $ p $ of size $ n $ . There are $ q $ queries of three types coming to you: 1. For given numbers $ l $ and $ r $ , calculate the sum in array $ a $ on the segment from $ l $ to $ r $ : $ \sum\limits_{i=l}^{r} a_i $ . 2. You are given two numbers $ v $ and $ x $ . Let's build a directed graph from the permutation $ p $ : it has $ n $ vertices and $ n $ edges $ i \to p_i $ . Let $ C $ be the set of vertices that are reachable from $ v $ in this graph. You should add $ x $ to all $ a_u $ such that $ u $ is in $ C $ . 3. You are given indices $ i $ and $ j $ . You should swap $ p_i $ and $ p_j $ . 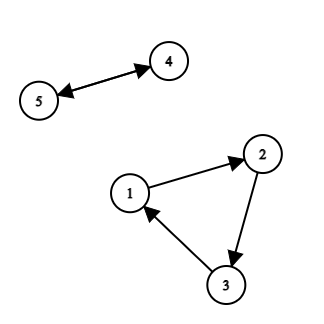The graph corresponding to the permutation $ [2, 3, 1, 5, 4] $ .Please, process all queries and print answers to queries of type $ 1 $ .

The first line contains a single integer $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) — the size of the array and permutation. The second line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ -10^8 \le a_i \le 10^8 $ ). The third line contains $ n $ distinct integers $ p_1, p_2, \ldots, p_n $ ( $ 1 \le p_i \le n $ ). The fourth line contains a single integer $ q $ — the number of queries ( $ 1 \le q \le 2 \cdot 10^5 $ ). Next $ q $ lines contain description of queries. The $ i $ -th of them starts with an integer $ t_i $ ( $ 1 \le t_i \le 3 $ ) — the query type. - If $ t_i = 1 $ , then the $ i $ -th line also contains two integers $ l $ , $ r $ ( $ 1 \le l \le r \le n $ ). - If $ t_i = 2 $ , then the $ i $ -th line also contains two integers $ v $ , $ x $ ( $ 1 \le v \le n $ , $ -10^8 \le x \le 10^8 $ ). - If $ t_i = 3 $ , then the $ i $ -th line also contains also two integers $ i $ , $ j $ ( $ 1 \le i, j \le n $ ).

For every first type query, print a single integer — the answer to this query.

In the first example: The graph corresponding to the initial permutation.There are $ 6 $ queries. 1. The sum on the segment from $ 1 $ to $ 5 $ is $ a_1 + a_2 + a_3 + a_4 + a_5 = 6 + 9 + (-5) + 3 + 0 = 13 $ . 2. If we start from $ 1 $ , we can reach $ \{1, 2, 3\} $ . After this query $ a $ is: $ [7, 10, -4, 3, 0] $ . 3. The sum on the segment from $ 1 $ to $ 5 $ is $ a_1 + a_2 + a_3 + a_4 + a_5 = 6 + 9 + (-5) + 3 + 0 = 16 $ . 4. After this query $ p = [4, 3, 1, 5, 2] $ . 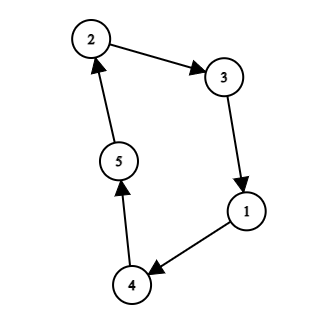The graph corresponding to the new permutation. 5. If we start from $ 2 $ , we can reach $ \{1, 2, 3, 4, 5\} $ . After this query $ a $ is: $ [6, 9, -5, 2, -1] $ . 6. The sum on the segment from $ 1 $ to $ 5 $ is $ a_1 + a_2 + a_3 + a_4 + a_5 = 6 + 9 + (-5) + 2 + (-1) = 11 $ .