CF1588F Jumping Through the Array
题目描述
给定一个大小为 $n$ 的整数数组 $a$ 和一个大小为 $n$ 的排列 $p$。有 $q$ 个三种类型的操作:
1. 给定 $l$ 和 $r$,计算数组 $a$ 在区间 $[l, r]$ 上的和:$\sum\limits_{i=l}^{r} a_i$。
2. 给定 $v$ 和 $x$。根据排列 $p$ 构建一个有向图:该图有 $n$ 个顶点和 $n$ 条边 $i \to p_i$。设 $C$ 为从 $v$ 出发可达的所有顶点集合。你需要将 $x$ 加到所有 $a_u$,其中 $u$ 属于 $C$。
3. 给定下标 $i$ 和 $j$,交换 $p_i$ 和 $p_j$。
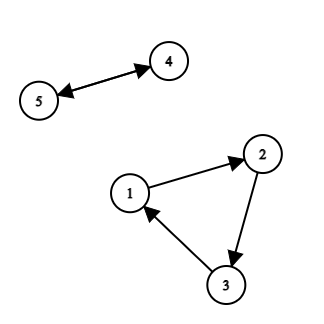 上图为排列 $[2, 3, 1, 5, 4]$ 对应的有向图。请处理所有操作,并输出所有第一类操作的答案。
输入格式
第一行包含一个整数 $n$($1 \le n \le 2 \cdot 10^5$),表示数组和排列的大小。
第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$($-10^8 \le a_i \le 10^8$)。
第三行包含 $n$ 个互不相同的整数 $p_1, p_2, \ldots, p_n$($1 \le p_i \le n$)。
第四行包含一个整数 $q$,表示操作的数量($1 \le q \le 2 \cdot 10^5$)。
接下来的 $q$ 行,每行描述一个操作。第 $i$ 行以一个整数 $t_i$($1 \le t_i \le 3$)开头,表示操作类型。
- 如果 $t_i = 1$,该行还包含两个整数 $l$、$r$($1 \le l \le r \le n$)。
- 如果 $t_i = 2$,该行还包含两个整数 $v$、$x$($1 \le v \le n$,$-10^8 \le x \le 10^8$)。
- 如果 $t_i = 3$,该行还包含两个整数 $i$、$j$($1 \le i, j \le n$)。
输出格式
对于每个第一类操作,输出一个整数,表示该操作的答案。
说明/提示
在第一个样例中:
 这是初始排列对应的有向图。共有 $6$ 个操作。
1. 区间 $1$ 到 $5$ 的和为 $a_1 + a_2 + a_3 + a_4 + a_5 = 6 + 9 + (-5) + 3 + 0 = 13$。
2. 从 $1$ 出发可达 $\{1, 2, 3\}$。操作后 $a$ 变为 $[7, 10, -4, 3, 0]$。
3. 区间 $1$ 到 $5$ 的和为 $a_1 + a_2 + a_3 + a_4 + a_5 = 7 + 10 + (-4) + 3 + 0 = 16$。
4. 操作后 $p = [4, 3, 1, 5, 2]$。 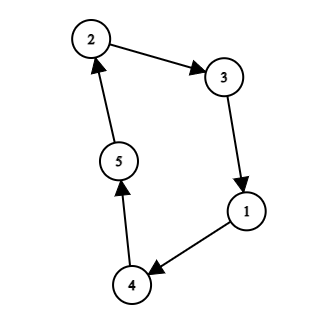 这是新排列对应的有向图。
5. 从 $2$ 出发可达 $\{1, 2, 3, 4, 5\}$。操作后 $a$ 变为 $[6, 9, -5, 2, -1]$。
6. 区间 $1$ 到 $5$ 的和为 $a_1 + a_2 + a_3 + a_4 + a_5 = 6 + 9 + (-5) + 2 + (-1) = 11$。
由 ChatGPT 4.1 翻译