CF1592C Bakry and Partitioning

### 题目背景 Bakry 遇到了一道题，但他懒得做了，于是他想让你帮他做。 一棵树有 $n$ 个节点，第 $i$ 个节点的点权为 $a_i$ 。（注：树是一个有 $n$ 个节点、$n-1$ 条边的连通图） 你需要回答：能不能选择这棵树中的至少 $1$ 条边、至多 $k-1$ 条边删除，使得删除完这些边的树满足以下条件： - 每个联通块的点权异或和相等

每个询问的第一行包含两个正整数 $n$ 和 $k\ (2\leq k \leq n \leq 10^5)$ 。 每个询问的第二行包含 $n$ 个整数，分别为 $a_1, a_2, ..., a_n\ (1\leq a_i \leq 10^9)$ 。 接下来的 $n-1$ 行中的第 $i$ 行包含两个整数 $u_i$ 和 $v_i\ (1\leq u_i, v_i\leq n, u_i\neq v_i)$，代表 $u_i$ 和 $v_i$ 之间有一条边。 保证给定的图是一棵树。 保证所有询问里的 $n$ 的和不超过 $2\cdot 10^5$ 。

对于每个询问，你需要在单独的一行中输出一个字符串。如果这个询问给出的数据满足题目条件，输出 `YES` 。否则，输出 `NO` 。 温馨小提示：本题输出不区分大小写。 ###### Translated by [\_FILARET\_](https://www.luogu.com.cn/user/84121)

It can be shown that the objection is not achievable for first, third, and fifth test cases. In the second test case, you can just remove all the edges. There will be $ 5 $ connected components, each containing only one node with value $ 3 $ , so the bitwise XORs will be $ 3 $ for all of them. In the fourth test case, this is the tree: 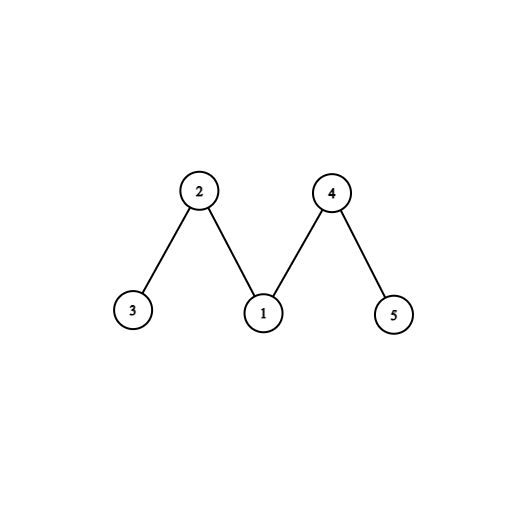. You can remove an edge $ (4,5) $ The bitwise XOR of the first component will be, $ a_1 \oplus a_2 \oplus a_3 \oplus a_4 = 1 \oplus 6 \oplus 4 \oplus 1 = 2 $ (where $ \oplus $ denotes the bitwise XOR). The bitwise XOR of the second component will be, $ a_5 = 2 $ .