CF1592D Hemose in ICPC ?

这是一个交互题！ 在上一次区域赛中，Hemose、ZeyadKhattab 和 YahiaSherif 组成的 Carpe Diem 队由于某些未知原因未能晋级 ICPC。比赛结束后，Hemose 非常难过，度过了糟糕的一天，但 ZeyadKhattab 很聪明，也很了解 Hemose，不想看到他难过。 Zeyad 知道 Hemose 喜欢树上问题，于是给了他一个带有特殊设备的树上问题。 Hemose 有一棵带权树，包含 $n$ 个节点和 $n-1$ 条边。不幸的是，Hemose 不记得每条边的权值了。 我们定义 $Dist(u, v)$（$u \neq v$）为从节点 $u$ 到节点 $v$ 的路径上所有边权的最大公约数。 Hemose 有一个特殊设备。Hemose 可以向设备输入一个节点集合，设备会返回该集合中任意两点间 $Dist$ 的最大值。更正式地说，若 Hemose 给设备一个节点集合 $S$，设备会返回所有 $u, v \in S$ 且 $u \neq v$ 的 $Dist(u, v)$ 的最大值。 Hemose 最多可以使用该设备 $12$ 次，他想找到任意一对不同的节点 $a, b$，使得 $Dist(a, b)$ 尽可能大。你能帮帮他吗？

首先输入一个整数 $n$（$2 \le n \le 10^3$），表示树的节点数。 接下来 $n-1$ 行，每行两个整数 $u_i$ 和 $v_i$（$1 \leq u_i, v_i \leq n$，$u_i \neq v_i$），表示节点 $u_i$ 和 $v_i$ 之间有一条边。 保证所有边的权值 $\leq 10^9$。 保证给定的图是一棵树。 现在你可以开始进行询问。每次你可以询问一个包含 $k$ 个节点的集合 $v_1, v_2, \ldots, v_k$（$2 \le k \le n$，$1 \le v_i \le n$，所有 $v_i$ 互不相同），输出： ? $k$ $v_1$ $v_2$ $\ldots$ $v_k$ 然后你会收到一个整数 $x$，表示所有 $1 \le i, j \le k$ 且 $i \neq j$ 的 $Dist(v_i, v_j)$ 的最大值。 当你找到一对 $a$ 和 $b$（$1 \le a, b \le n$，$a \neq b$），使得 $Dist(a, b)$ 达到最大时，按如下格式输出答案： ! $a$ $b$ 输出答案不计入 $12$ 次询问限制。 如果有多组 $(a, b)$ 使得 $Dist(a, b)$ 相同且最大，你可以输出任意一组。 每次输出询问后不要忘记输出换行并刷新输出缓冲区，否则会导致“Idleness limit exceeded”。具体操作如下： - C++：fflush(stdout) 或 cout.flush() - Java：System.out.flush() - Pascal：flush(output) - Python：stdout.flush() - 其它语言请查阅相关文档 Hack 格式 要 hack 一个解，使用如下格式： 第一行输入一个整数 $n$（$2 \leq n \leq 10^3$），表示节点数。 接下来 $n-1$ 行，每行三个整数 $u_i$、$v_i$、$w_i$（$1 \le u_i, v_i \le n$，$u_i \ne v_i$，$1 \le w \le 10^9$），表示 $u_i$ 和 $v_i$ 之间有一条权值为 $w_i$ 的边。 这 $n-1$ 条边必须构成一棵树。

（见上文，交互式输出，具体格式详见题目描述。）

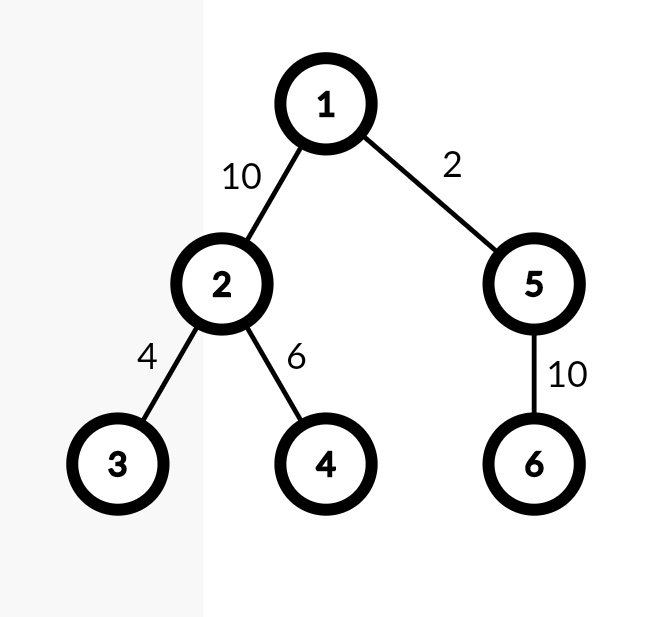
第一组样例中的树如下：  由 ChatGPT 4.1 翻译