CF1605D Treelabeling

Eikooc 和 Sushi 玩一个游戏。 游戏在一棵有 $n$ 个节点的树上进行，节点编号为 $1$ 到 $n$。回忆一下，一棵有 $n$ 个节点的树是一个无向连通图，包含 $n-1$ 条边。 他们轮流移动树上的一个棋子。Eikooc 先手，可以将棋子放在任意一个她选择的节点上。接下来 Sushi 移动棋子，然后是 Eikooc，再是 Sushi，如此交替。在第一步之后，每一回合，玩家必须将棋子移动到一个节点 $u$，满足以下条件： - $u$ 与当前棋子所在的节点 $v$ 相邻； - $u$ 尚未被访问过； - $u \oplus v \leq \min(u, v)$。 这里 $x \oplus y$ 表示整数 $x$ 和 $y$ 的[按位异或](https://en.wikipedia.org/wiki/Bitwise_operation#XOR)操作。 两位玩家都会采取最优策略。无法移动棋子的玩家判负。 下面是一些演示游戏规则的例子。 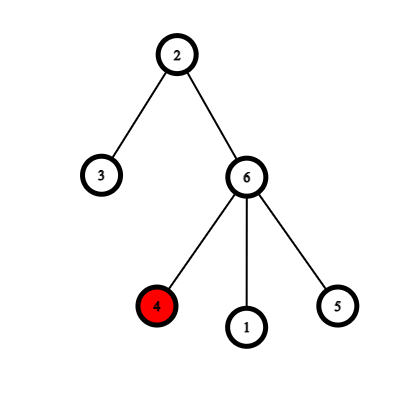 假设 Eikooc 首先将棋子放在节点 $4$。Sushi 随后将棋子移动到节点 $6$，该节点未被访问且与 $4$ 相邻。同时 $6 \oplus 4 = 2 \leq \min(6, 4)$。接下来，Eikooc 将棋子移动到节点 $5$，该节点未被访问且与 $6$ 相邻，同时 $5 \oplus 6 = 3 \leq \min(5, 6)$。Sushi 已无可走之路，因此她输掉了游戏。 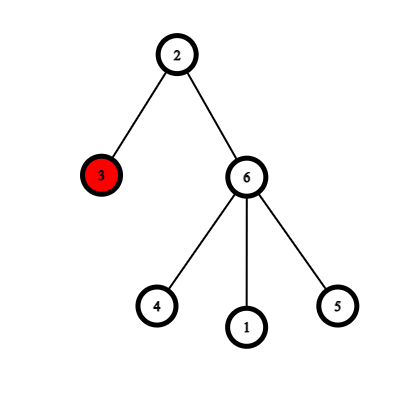 假设 Eikooc 首先将棋子放在节点 $3$。Sushi 将棋子移动到节点 $2$，该节点未被访问且与 $3$ 相邻，同时 $3 \oplus 2 = 1 \leq \min(3, 2)$。Eikooc 不能将棋子移动到节点 $6$，因为 $6 \oplus 2 = 4 \nleq \min(6, 2)$。由于 Eikooc 无法继续移动棋子，她输掉了游戏。 在游戏开始前，Eikooc 决定偷偷地重新标号树上的节点以利于自己。形式化地说，重新标号是一个长度为 $n$ 的排列 $p$（一个包含 $1$ 到 $n$ 的每个整数恰好一次的序列），其中 $p_i$ 表示节点 $i$ 的新编号。 她希望最大化她在第一回合可以选择并保证获胜的节点数。请你帮助 Eikooc 找到一种重新标号方式，使她能实现这一目标。

第一行包含一个整数 $t~(1 \le t \le 10^5)$，表示测试用例的数量。每个测试用例的描述如下： 每个测试用例的第一行包含一个整数 $n~(1 \le n \le 2 \cdot 10^5)$，表示树的节点数。 接下来的 $n-1$ 行，每行包含两个整数 $u$ 和 $v$ $(1 \le u, v \le n; u \neq v)$，表示节点 $u$ 和节点 $v$ 之间有一条边。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一种可行的重新标号方式——一个长度为 $n$ 的排列，使得 Eikooc 能够选择的、保证获胜的节点数最大化。如果有多种方案，可以输出任意一种。

在第一个测试用例中，Eikooc 只有一个选择。Eikooc 选择该节点后，Sushi 无法再移动棋子，因此 Eikooc 获胜。 在第二个测试用例中，$1 \oplus 2 = 3 \nleq \min(1, 2)$。因此，无论 Eikooc 选择哪一个节点，Sushi 都无法移动棋子，Eikooc 获胜。$\{1, 2\}$ 和 $\{2, 1\}$ 都是最优的重新标号方式。 由 ChatGPT 4.1 翻译