CF1606F Tree Queries

给定一棵包含 $n$ 个顶点的树。回忆一下，树是一种无向、连通且无环的图。给定的树以顶点 $1$ 作为根节点。 你需要处理 $q$ 个查询。每个查询给定树上的一个顶点 $v$ 和一个整数 $k$。 对于每个查询，你可以以任意顺序删除树上的任意顶点，但不能删除根节点和顶点 $v$。当一个顶点被删除时，它的所有子节点会变为它父节点的子节点。你需要通过合理删除顶点，使得 $c(v) - m \cdot k$ 的值最大（其中 $c(v)$ 表示最终顶点 $v$ 的子节点数，$m$ 表示你删除的顶点数）。请输出你能获得的最大值。 各个查询互不影响：你在处理某个查询时对树的修改不会影响其他查询。

第一行包含一个整数 $n$（$1 \le n \le 2 \cdot 10^5$），表示树的顶点数。 接下来 $n-1$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$1 \le x_i, y_i \le n$，$x_i \ne y_i$），表示第 $i$ 条边的两个端点。这些边构成一棵树。 接下来一行包含一个整数 $q$（$1 \le q \le 2 \cdot 10^5$），表示查询的数量。 接下来 $q$ 行，每行包含两个整数 $v_j$ 和 $k_j$（$1 \le v_j \le n$，$0 \le k_j \le 2 \cdot 10^5$），分别表示第 $j$ 个查询的参数。

对于每个查询，输出一个整数，表示你能获得的最大 $c(v) - m \cdot k$ 的值。

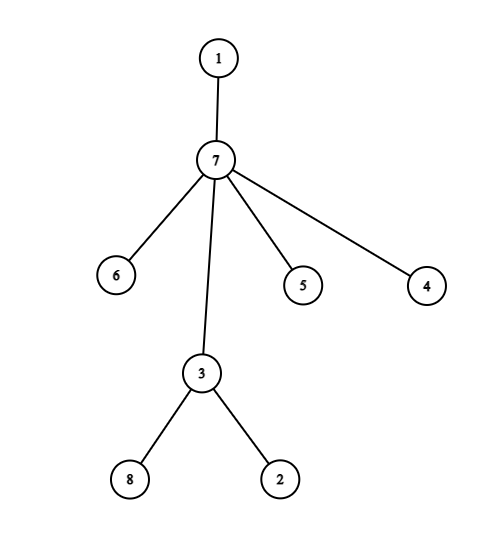
下图展示了第一个样例中的树结构：  各个查询的答案如下： 1. $v=1, k=0$：你可以删除顶点 $7$ 和 $3$，此时顶点 $1$ 有 $5$ 个子节点（$2$、$4$、$5$、$6$、$8$），得分为 $5-2\cdot 0=5$； 2. $v=1, k=2$：你可以删除顶点 $7$，此时顶点 $1$ 有 $4$ 个子节点（$3$、$4$、$5$、$6$），得分为 $4-1\cdot 2=2$； 3. $v=1, k=3$：你不应删除任何顶点，此时顶点 $1$ 只有一个子节点（$7$），得分为 $1-0\cdot 3=1$； 4. $v=7, k=1$：你可以删除顶点 $3$，此时顶点 $7$ 有 $5$ 个子节点（$2$、$4$、$5$、$6$、$8$），得分为 $5-1\cdot 1=4$； 5. $v=5, k=0$：无论如何操作，顶点 $5$ 都没有子节点，得分为 $0$； 6. $v=7, k=200000$：你不应删除任何顶点，此时顶点 $7$ 有 $4$ 个子节点（$3$、$4$、$5$、$6$），得分为 $4-0\cdot 200000=4$。 由 ChatGPT 4.1 翻译