CF1610D Not Quite Lee

Lee 最近无法入睡，因为他总是做噩梦。其中一个噩梦（关于一场不平衡的全球比赛）让他决定反击，于是他提出了下面这个问题（你需要解决它）来平衡比赛，希望能让自己从噩梦中解脱出来。 一个非空数组 $b_1, b_2, \ldots, b_m$ 被称为**好的**，需要存在 $m$ 个序列满足以下条件： - 第 $i$ 个序列由 $b_i$ 个连续的整数组成（例如，若 $b_i = 3$，则第 $i$ 个序列可以是 $(-1, 0, 1)$ 或 $(-5, -4, -3)$，但不能是 $(0, -1, 1)$ 或 $(1, 2, 3, 4)$）。 - 假设第 $i$ 个序列的整数和为 $sum_i$，要求 $sum_1 + sum_2 + \cdots + sum_m$ 等于 $0$。 给定一个数组 $a_1, a_2, \cdots, a_n$，它有 $2^n - 1$ 个非空子序列。请计算其中有多少个子序列是好的。由于这个数字可能非常大，输出它对 $10^9 + 7$ 取模的结果。 数组 $c$ 是数组 $d$ 的子序列，当且仅当 $c$ 可以通过从 $d$ 中删除若干（可能为零或全部）元素得到。

第一行包含一个整数 $n$（$2 \leq n \leq 2 \times 10^5$）表示数组 $a$ 的大小。 第二行包含 $n$ 个整数 $a_1, a_2, \cdots, a_n$（$1 \leq a_i \leq 10^9$），表示数组的元素。

输出一个整数，表示好的非空子序列的数量，答案对 $10^9 + 7$ 取模。

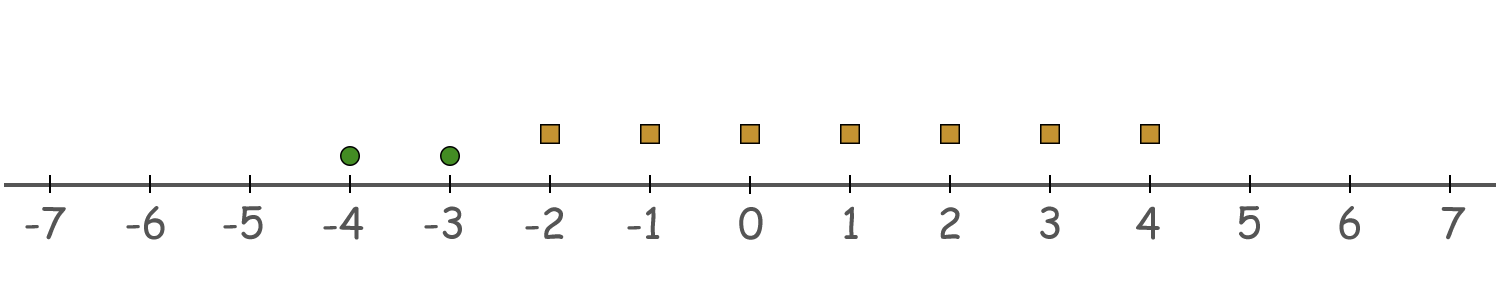
对于样例一，两个好的子序列的例子是 $[2, 7]$ 和 $[2, 2, 4, 7]$： 对于 $b = [2, 7]$，我们可以使用 $(-3, -4)$ 作为第一个序列，$(-2, -1, \cdots, 4)$ 作为第二个序列。注意子序列 $[2, 7]$ 在 $[2, 2, 4, 7]$ 中出现了两次，因此需要计数两次。  **绿色圆圈表示 $(-3, -4)$，橙色方块表示 $(-2, -1, \cdots, 4)$。** 对于 $b = [2, 2, 4, 7]$，以下序列满足条件：$(-1, 0),(-3, -2),(0, 1, 2, 3)$ 和 $(-3, -2, \cdots, 3)$。