CF1611D Weights Assignment For Tree Edges

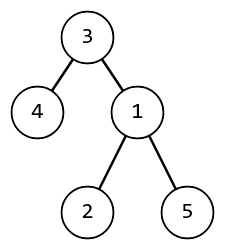
给定一棵有 $n$ 个顶点的有根树。顶点编号为 $1$ 到 $n$。任意顶点都可以作为树的根。 树是一个无环连通无向图。有根树是在树中选定一个顶点作为根。 树通过祖先数组 $b$ 给出，包含 $n$ 个数：$b_i$ 表示编号为 $i$ 的顶点的祖先。顶点 $u$ 的祖先是从 $u$ 到根的简单路径上的下一个顶点。例如，从 $5$ 到 $3$（根）的简单路径上，下一个顶点是 $1$，所以 $5$ 的祖先是 $1$。 根没有祖先，因此对于根，$b_i = i$（根是唯一满足 $b_i = i$ 的顶点）。 例如，如果 $n=5$，$b=[3, 1, 3, 3, 1]$，则树结构如下所示。  这是 $n=5$ 时的有根树示例，树的根为顶点 $3$。 给定一个数组 $p$，它是树顶点的一个排列。如果可能，请为树的边分配任意正整数权值，使得按从根到各顶点的距离排序后，顶点顺序恰好为给定的排列 $p$。 换句话说，对于给定的顶点排列 $p$，需要选择边权，使得对每个 $i$（$1 \leq i < n$）都有 $dist[p_i] < dist[p_{i+1}]$。其中 $dist[u]$ 表示从根到 $u$ 路径上所有边权之和。特别地，根的 $dist[u]=0$。 例如，假设 $p=[3, 1, 2, 5, 4]$，则如下边权满足要求： - 边 $(3, 4)$ 权值为 $102$； - 边 $(3, 1)$ 权值为 $1$； - 边 $(1, 2)$ 权值为 $10$； - 边 $(1, 5)$ 权值为 $100$。 此时各顶点到根的距离数组为 $dist=[1,11,0,102,101]$。按距离从小到大排序，顶点顺序正好为 $p$。 请输出所需的边权，或判断是否无法分配权值。如果有多种方案，输出任意一种。

输入的第一行为整数 $t$（$1 \leq t \leq 10^4$），表示测试数据组数。 每组测试数据包含三行。 第一行为整数 $n$（$1 \leq n \leq 2 \cdot 10^5$），表示树的顶点数。 第二行为 $n$ 个整数 $b_1, b_2, \dots, b_n$（$1 \leq b_i \leq n$），表示祖先数组。保证 $b$ 数组编码的是一棵有根树。 第三行为排列 $p$：$n$ 个不同的整数 $p_1, p_2, \dots, p_n$（$1 \leq p_i \leq n$）。 保证所有测试数据中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每组测试数据，输出一行答案。 如果存在解，输出 $n$ 个整数 $w_1, w_2, \dots, w_n$，其中 $w_i$ 表示从 $b_i$ 到 $i$ 的边的权值。对于根节点没有这样的边，$w_i=0$。对于其他顶点，$w_i$ 需满足 $1 \leq w_i \leq 10^9$。$w_i$ 之间可以有相等的数，但从根到每个顶点的路径权值之和必须各不相同，并且满足给定的排列顺序。 如果有多种方案，输出任意一种。 如果不存在解，输出 $-1$。

样例的第一组数据已在题目描述中分析。 样例的第二组数据无法分配正权值使得顶点排列满足要求。 由 ChatGPT 4.1 翻译