CF1615E Purple Crayon

两位玩家，Red 和 Blue，又开始了他们的游戏，这一次他们用蜡笔在一棵有根树上涂色！这对调皮的搭档现在正在破坏一棵有根树，通过给节点涂色来玩他们最喜欢的游戏。 游戏规则如下：有一棵大小为 $n$ 的树，以节点 $1$ 为根，每个节点初始时都是白色的。Red 和 Blue 各有一次回合，Red 先手。 在 Red 的回合中，他可以进行如下操作任意次： - 选择有根树的任意一个子树，并将该子树中的所有节点涂成红色。 但是，为了公平起见，Red 只允许最多给 $k$ 个节点涂红。换句话说，Red 的回合结束后，最多有 $k$ 个节点被涂成红色。然后轮到 Blue。Blue 可以进行如下操作任意次： - 选择有根树的任意一个子树，并将该子树中的所有节点涂成蓝色。但他不能选择包含已经被涂成红色的节点的子树，否则这些节点会变成紫色，而没人喜欢紫色蜡笔。 注意：Blue 可以涂色的节点数量没有限制，只要他不涂到已经被涂成红色的节点即可。两人回合结束后，游戏得分规则如下：设 $w$ 为白色节点数，$r$ 为红色节点数，$b$ 为蓝色节点数。游戏得分为 $w \cdot (r - b)$。 Red 希望最大化得分，Blue 希望最小化得分。如果双方都采取最优策略，最终的游戏得分是多少？

第一行包含两个整数 $n$ 和 $k$（$2 \le n \le 2 \cdot 10^5$；$1 \le k \le n$），分别表示树的节点数和最多可被涂成红色的节点数。 接下来的 $n-1$ 行，每行包含两个用空格分隔的整数 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n$；$u_i \neq v_i$），表示树的第 $i$ 条边。 保证所给边构成一棵树。

输出一个整数，表示双方都采取最优策略时游戏的最终得分。

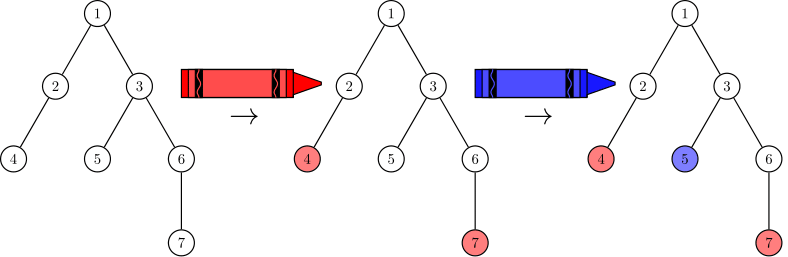
在第一个测试用例中，最优策略如下： - Red 选择将节点 $2$ 和 $3$ 的子树涂红。 - Blue 选择将节点 $4$ 的子树涂蓝。 最终，节点 $2$ 和 $3$ 被涂成红色，节点 $4$ 被涂成蓝色，节点 $1$ 仍为白色。游戏得分为 $1 \cdot (2 - 1) = 1$。 在第二个测试用例中，最优策略如下： - Red 选择将节点 $4$ 的子树涂红，这样节点 $4$ 和 $5$ 都被涂成红色。 - Blue 没有可选的操作，因此没有节点被涂成蓝色。 最终，节点 $4$ 和 $5$ 被涂成红色，节点 $1$、$2$ 和 $3$ 仍为白色。游戏得分为 $3 \cdot (2 - 0) = 6$。 对于第三个测试用例：  游戏得分为 $4 \cdot (2 - 1) = 4$。 由 ChatGPT 4.1 翻译