Unusual Minesweeper

### 题目描述 Polycarp 非常喜欢玩扫雷游戏。最近，他发现了一个类似的游戏，也有这样的规则。 场地上有一些地雷，每个地雷的坐标 $(x_i,y_i)$ 都是已知的，每个坐标都有以秒为单位的倒计时，之后地雷就会爆炸。爆炸后，地雷会引爆所有与地雷垂直和水平距离在 $k$ 之内的地雷，结果就是我们得到了形状为"+"的爆炸。而一次爆炸可以引起新的爆炸，每次都是这样。 此外，从 $0$ 秒开始，Polycarp 可以每秒引爆任意一个地雷，连锁反应随之发生。需要注意的是，地雷会立刻爆炸并立刻引爆其它地雷。 Polycarp 想创造一个新纪录，请你帮他计算一下，他最快能在多少秒内引爆所有地雷？ ### 输入格式 输入的第一行包含一个整数 $t$ ($1 \le t \le 10^4$)——测试数据的组数。 每一组测试数据前都有一个空行。 接下来一行包含两个整数 $n,k(1 \le n \le 2 \cdot 10^5 ,0 \le k \le 10^9)$——地雷的数量和爆炸的范围。 接下来 $n$ 行，其中第 $i$ 行包含第 $i$ 颗地雷的 $x$ 和 $y$ 坐标，以及它爆炸的时间$(-10^9 \le x, y \le 10 ^9，0 \le timer \le 10^9)$。保证所有地雷的坐标都不同。 保证所有测试数据的 $n$ 之和不超过 $2 \cdot 10^5$。 ### 输出格式 共 $t$ 行，每行分别表示对应输入数据集合的答案——引爆所有地雷所需的最小时间。 $\\$ By 御坂10029号$\\$2022/01/29

Polycarp is very fond of playing the game Minesweeper. Recently he found a similar game and there are such rules. There are mines on the field, for each the coordinates of its location are known ( $ x_i, y_i $ ). Each mine has a lifetime in seconds, after which it will explode. After the explosion, the mine also detonates all mines vertically and horizontally at a distance of $ k $ (two perpendicular lines). As a result, we get an explosion on the field in the form of a "plus" symbol ('+'). Thus, one explosion can cause new explosions, and so on. Also, Polycarp can detonate anyone mine every second, starting from zero seconds. After that, a chain reaction of explosions also takes place. Mines explode instantly and also instantly detonate other mines according to the rules described above. Polycarp wants to set a new record and asks you to help him calculate in what minimum number of seconds all mines can be detonated.

The first line of the input contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases in the test. An empty line is written in front of each test suite. Next comes a line that contains integers $ n $ and $ k $ ( $ 1 \le n \le 2 \cdot 10^5 $ , $ 0 \le k \le 10^9 $ ) — the number of mines and the distance that hit by mines during the explosion, respectively. Then $ n $ lines follow, the $ i $ -th of which describes the $ x $ and $ y $ coordinates of the $ i $ -th mine and the time until its explosion ( $ -10^9 \le x, y \le 10^9 $ , $ 0 \le timer \le 10^9 $ ). It is guaranteed that all mines have different coordinates. It is guaranteed that the sum of the values $ n $ over all test cases in the test does not exceed $ 2 \cdot 10^5 $ .

Print $ t $ lines, each of the lines must contain the answer to the corresponding set of input data — the minimum number of seconds it takes to explode all the mines.

3

5 0
0 0 1
0 1 4
1 0 2
1 1 3
2 2 9

5 2
0 0 1
0 1 4
1 0 2
1 1 3
2 2 9

6 1
1 -1 3
0 -1 9
0 1 7
-1 0 1
-1 1 9
-1 -1 7

2
1
0

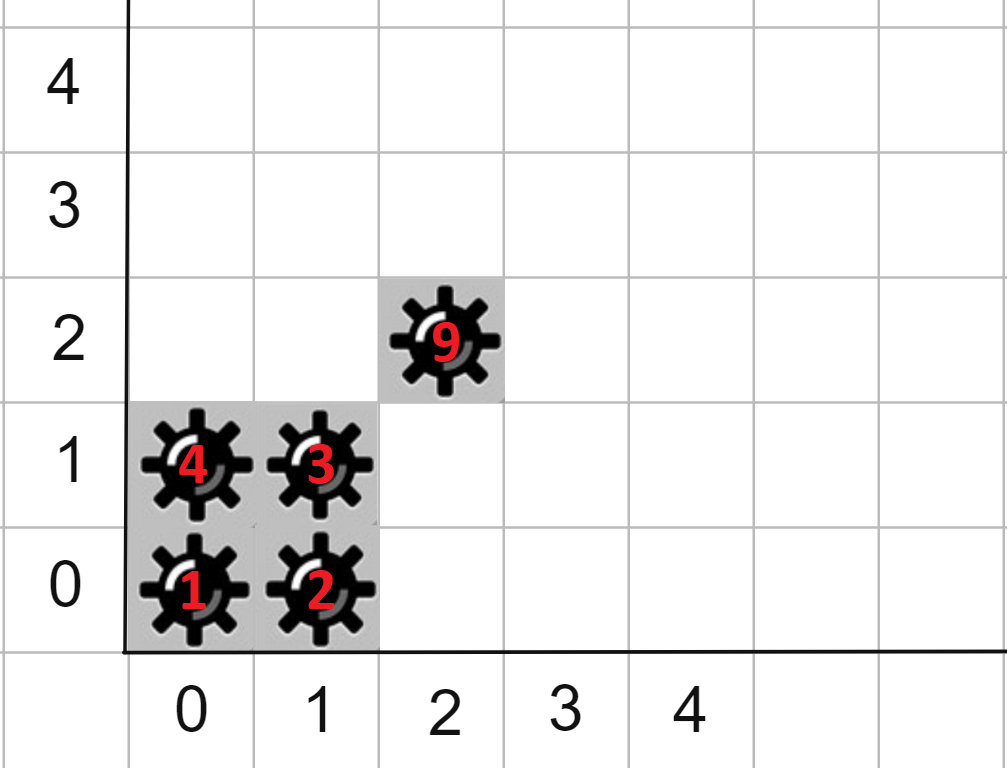Picture from examplesFirst example: - $ 0 $ second: we explode a mine at the cell $ (2, 2) $ , it does not detonate any other mine since $ k=0 $ . - $ 1 $ second: we explode the mine at the cell $ (0, 1) $ , and the mine at the cell $ (0, 0) $ explodes itself. - $ 2 $ second: we explode the mine at the cell $ (1, 1) $ , and the mine at the cell $ (1, 0) $ explodes itself. 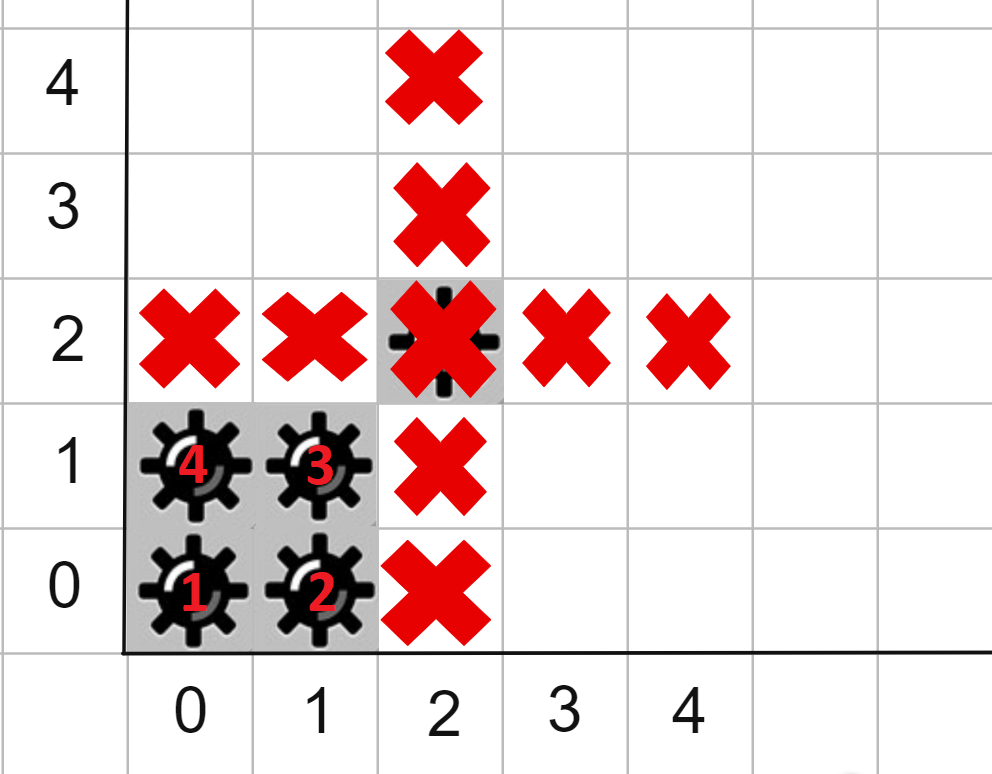Second example: - $ 0 $ second: we explode a mine at the cell $ (2, 2) $ we get: - $ 1 $ second: the mine at coordinate $ (0, 0) $ explodes and since $ k=2 $ the explosion detonates mines at the cells $ (0, 1) $ and $ (1, 0) $ , and their explosions detonate the mine at the cell $ (1, 1) $ and there are no mines left on the field.