CF1619G Unusual Minesweeper

Polycarp is very fond of playing the game Minesweeper. Recently he found a similar game and there are such rules. There are mines on the field, for each the coordinates of its location are known ( $ x_i, y_i $ ). Each mine has a lifetime in seconds, after which it will explode. After the explosion, the mine also detonates all mines vertically and horizontally at a distance of $ k $ (two perpendicular lines). As a result, we get an explosion on the field in the form of a "plus" symbol ('+'). Thus, one explosion can cause new explosions, and so on. Also, Polycarp can detonate anyone mine every second, starting from zero seconds. After that, a chain reaction of explosions also takes place. Mines explode instantly and also instantly detonate other mines according to the rules described above. Polycarp wants to set a new record and asks you to help him calculate in what minimum number of seconds all mines can be detonated.

The first line of the input contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases in the test. An empty line is written in front of each test suite. Next comes a line that contains integers $ n $ and $ k $ ( $ 1 \le n \le 2 \cdot 10^5 $ , $ 0 \le k \le 10^9 $ ) — the number of mines and the distance that hit by mines during the explosion, respectively. Then $ n $ lines follow, the $ i $ -th of which describes the $ x $ and $ y $ coordinates of the $ i $ -th mine and the time until its explosion ( $ -10^9 \le x, y \le 10^9 $ , $ 0 \le timer \le 10^9 $ ). It is guaranteed that all mines have different coordinates. It is guaranteed that the sum of the values $ n $ over all test cases in the test does not exceed $ 2 \cdot 10^5 $ .

Print $ t $ lines, each of the lines must contain the answer to the corresponding set of input data — the minimum number of seconds it takes to explode all the mines.

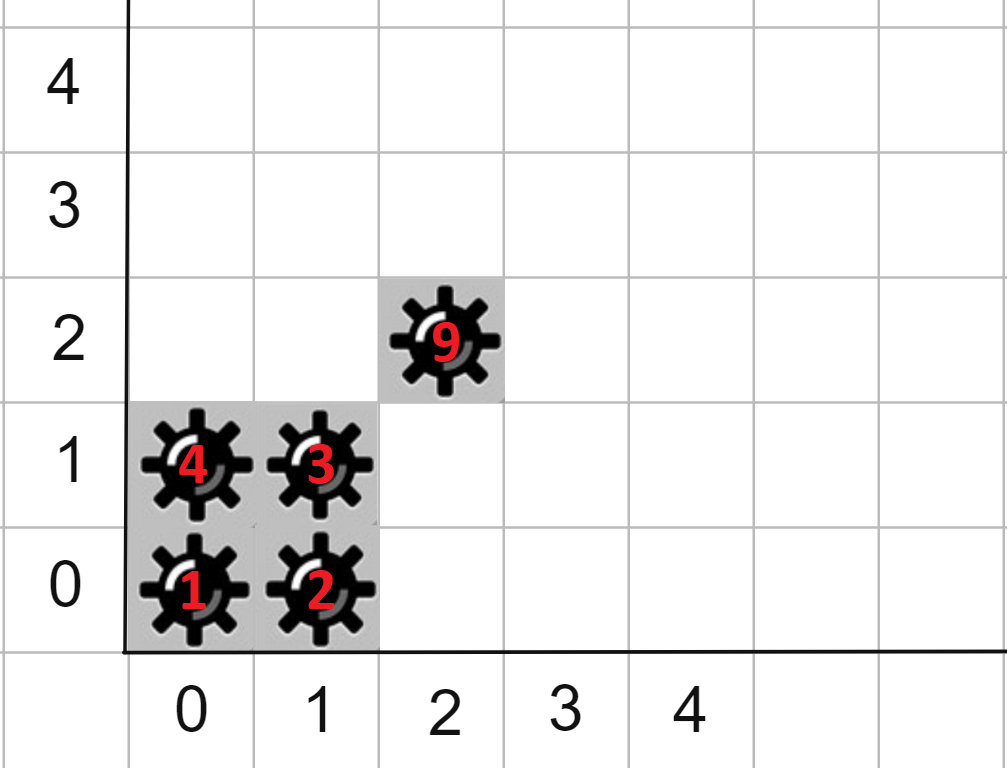Picture from examplesFirst example: - $ 0 $ second: we explode a mine at the cell $ (2, 2) $ , it does not detonate any other mine since $ k=0 $ . - $ 1 $ second: we explode the mine at the cell $ (0, 1) $ , and the mine at the cell $ (0, 0) $ explodes itself. - $ 2 $ second: we explode the mine at the cell $ (1, 1) $ , and the mine at the cell $ (1, 0) $ explodes itself. 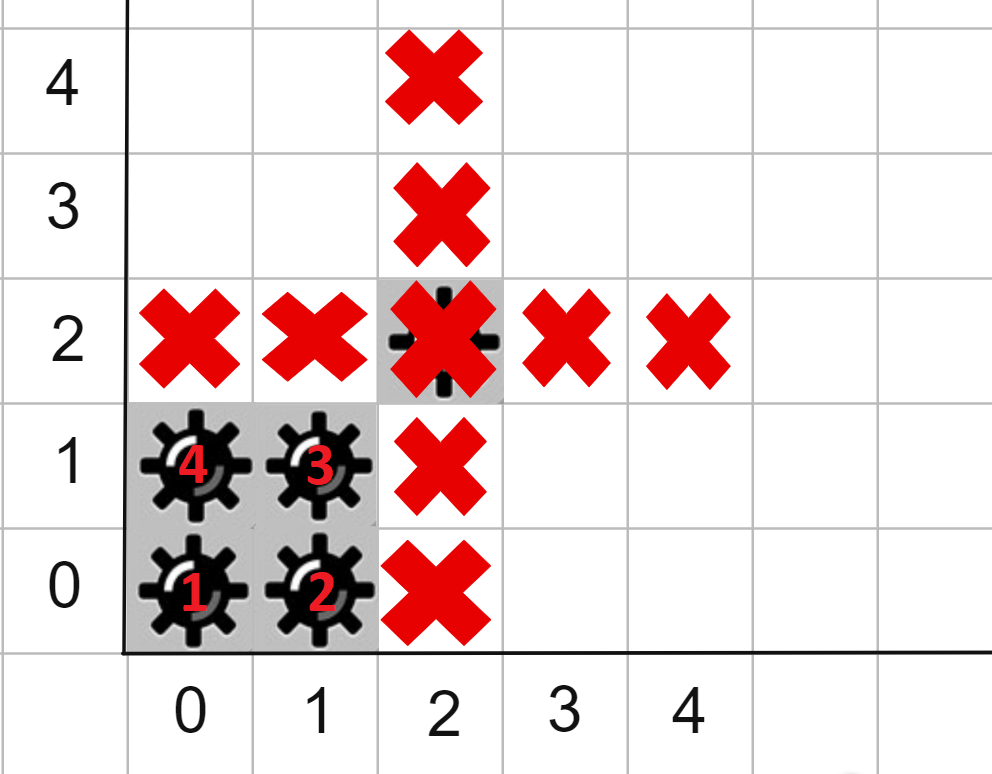Second example: - $ 0 $ second: we explode a mine at the cell $ (2, 2) $ we get: - $ 1 $ second: the mine at coordinate $ (0, 0) $ explodes and since $ k=2 $ the explosion detonates mines at the cells $ (0, 1) $ and $ (1, 0) $ , and their explosions detonate the mine at the cell $ (1, 1) $ and there are no mines left on the field.