CF1621A Stable Arrangement of Rooks

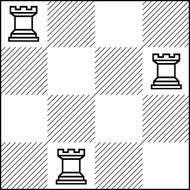
你有一个 $n \times n$ 的国际象棋棋盘和 $k$ 个车。棋盘的行编号为 $1$ 到 $n$（从上到下），列编号为 $1$ 到 $n$（从左到右）。格子 $(x, y)$ 表示第 $x$ 行第 $y$ 列的格子，其中 $1 \leq x \leq n$ 且 $1 \leq y \leq n$。 如果棋盘上的车的摆放方式满足没有任何一辆车能攻击到另一辆车，则称这种摆放方式是“好”的。 一辆车可以攻击所有与它在同一行或同一列的车。 如果一个“好”的摆放方式满足：存在一辆车可以移动到相邻的格子（即与当前格子有公共边的格子），使得摆放方式变得不是“好”的，则称这种摆放方式为“不稳定”的。否则，称为“稳定”的。这里，相邻的格子指的是有公共边的格子。  如图，在 $4 \times 4$ 的棋盘上有 $3$ 个车的这种摆放方式是“好”的，但不是“稳定”的：可以把 $(1, 1)$ 的车移动到相邻的 $(2, 1)$，此时 $(2, 1)$ 和 $(2, 4)$ 的车会互相攻击。 请你找出一种在 $n \times n$ 棋盘上摆放 $k$ 个车的“稳定”摆放方式，或者报告不存在这样的摆放方式。

第一行包含一个整数 $t$（$1 \leq t \leq 100$），表示测试用例的数量。 每个测试用例的第一行包含两个整数 $n$ 和 $k$（$1 \leq k \leq n \leq 40$），分别表示棋盘的大小和车的数量。

如果存在一种“稳定”的摆放方式，在棋盘上摆放 $k$ 个车，则输出 $n$ 行，每行由符号 . 和 R 组成。如果第 $i$ 行第 $j$ 列有车，则第 $i$ 行第 $j$ 个字符为 R，否则为 .。 如果有多种方案，可以输出任意一种。 如果不存在“稳定”的摆放方式，输出 $-1$。

在第一个测试用例中，你需要在 $3 \times 3$ 的棋盘上找到 $2$ 个车的“稳定”摆放方式。将它们放在 $(3, 1)$ 和 $(1, 3)$ 可以得到“稳定”的摆放。 在第二个测试用例中，可以证明无法在 $3 \times 3$ 的棋盘上放置 $3$ 个车，使其为“稳定”的摆放方式。 由 ChatGPT 4.1 翻译