CF1621H Trains and Airplanes

一个城市的铁路网络由 $n$ 个车站和 $n-1$ 条道路组成。这些车站和道路构成一棵树。车站 $1$ 是市中心。对于每条道路，你都知道火车通过这条道路所需的时间。你可以假设火车在车站停靠时不耗费时间。我们定义 $dist(v)$ 为火车从车站 $v$ 到车站 $1$ 所需的时间。 这个铁路网络被划分为若干个区域，区域名称为前 $k$ 个大写拉丁字母。第 $i$ 个车站所属的区域为 $z_i$。市中心属于 A 区。对于所有其他车站，保证从该车站到市中心的路径上的第一个车站要么在同一区域，要么在字典序更小的区域。任意一条道路完全归属于离市中心最远的端点所在的区域。 游客即将抵达机场，然后前往市中心。游客从车站 $v$ 到车站 $1$ 的旅程如下： - 在时刻 $0$，游客登上直达市中心的火车。旅程将持续 $dist(v)$ 分钟。 - 游客可以在任意时刻购买任意区域的车票。第 $i$ 个区域的车票价格为 $pass_i$ 欧元。 - 从旅程开始后每隔 $T$ 分钟（即在 $T, 2T, \ldots$ 时刻），检票系统会对游客进行检查。如果检查时游客在第 $i$ 个区域且没有该区域的车票，则需支付 $fine_i$ 欧元罚款。具体来说，游客所在的区域判定方式如下： - 如果游客在车站 $1$，则已到达市中心，无需支付罚款。 - 如果游客在车站 $u \neq 1$，则他在 $z_u$ 区域。 - 如果游客正在从车站 $x$ 前往与其直接相连的车站 $y$，则他在 $z_x$ 区域。 注意，游客在同一区域可能会多次被罚款。 游客总是选择使旅程总花费最小的购票和罚款方案。令 $f(v)$ 表示从车站 $v$ 出发的最小总花费。 不幸的是，游客并不知道各区域当前的 $pass_i$ 和 $fine_i$，也忘记了机场的位置。他会向你提出三种类型的询问： - $1\ i\ c$ —— 第 $i$ 个区域的车票价格变为 $c$。 - $2\ i\ c$ —— 第 $i$ 个区域的罚款变为 $c$。 - $3\ u$ —— 对当前的 $pass$ 和 $fine$，解决如下问题： - 给定车站 $u$，考虑所有满足下列条件的车站 $v$： - $z_v = z_u$ - 车站 $u$ 在从车站 $v$ 到车站 $1$ 的路径上 - 在假设游客已经拥有 $z_u$ 区域车票的前提下，求所有这样的 $v$ 中 $\min(f(v))$ 的值。

第一行包含一个整数 $n$（$2 \leq n \leq 2 \cdot 10^5$），表示车站数量。 接下来的 $n-1$ 行，每行包含三个整数 $v_i$、$u_i$、$t_i$（$1 \leq v_i, u_i \leq n, 1 \leq t_i \leq 10^9$），表示第 $i$ 条道路的两个端点及火车通过该道路所需时间。保证这些道路构成一棵树。 下一行包含一个整数 $k$（$1 \leq k \leq 26$），表示区域数量。 下一行包含 $n$ 个字符 $z_1z_2\ldots z_n$，其中 $z_i$ 表示第 $i$ 个车站所属的区域。保证满足题目第二段的条件。 下一行包含 $k$ 个整数 $pass_1, pass_2, \ldots, pass_k$（$1 \leq pass_i \leq 10^9$），表示初始的各区域车票价格。 下一行包含 $k$ 个整数 $fine_1, fine_2, \ldots, fine_k$（$1 \leq fine_i \leq 10^9$），表示初始的各区域罚款金额。 下一行包含一个整数 $T$（$1 \leq T \leq 10^9$），表示检票系统的检查间隔时间。 下一行包含一个整数 $q$（$1 \leq q \leq 2 \cdot 10^5$），表示询问数量。 接下来的 $q$ 行，每行一个询问，格式如题目描述所述。保证在第一、二类询问中 $i$ 是前 $k$ 个大写拉丁字母之一，$1 \leq c \leq 10^9$，在第三类询问中 $1 \leq u \leq n$。

对于每个第三类询问，输出对应的答案。

注意，罚款可能比车票便宜。 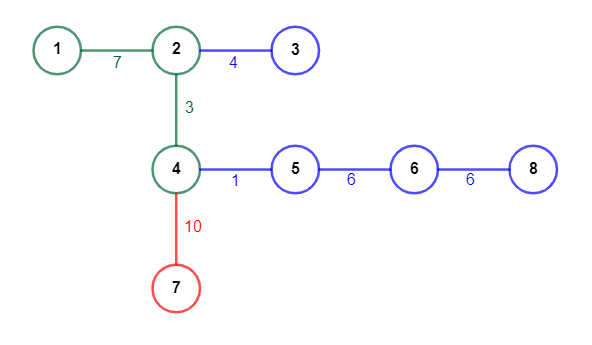 图为样例中的铁路网络。绿色表示 A 区的车站和道路，蓝色表示 B 区，红色表示 D 区。每条道路旁的数字表示火车通过该道路所需的时间。在第一个询问中，机场可能在车站 $2$ 或 $4$ 附近。旅途中游客始终在 A 区，且已持有该区车票，因此答案为 $0$。 第二个询问后，A 区车票价格变为 $10$。 第三个询问中，机场只能在车站 $3$ 附近。最优方案是购买 A 区车票。旅程的前 $3$ 秒游客在 B 区，然后进入 A 区，并在第 $4$ 秒和第 $8$ 秒被检查。由于已持有该区车票，无需罚款。 第四个询问后，A 区罚款变为 $3$。 第五个询问中，机场只能在车站 $7$，且 $f(7) = 6$。 第六个询问中，机场可能在车站 $6$ 或 $8$。由于 $f(6)=9$，$f(8)=6$，答案为 $6$。 由 ChatGPT 4.1 翻译