CF1623E Middle Duplication

给定一棵有 $n$ 个节点的二叉树。树的节点编号为 $1$ 到 $n$，根节点为 $1$ 号节点。每个节点可以没有子节点、只有左子节点、只有右子节点，或同时有左右子节点。为方便起见，记 $l_u$ 和 $r_u$ 分别为节点 $u$ 的左子节点和右子节点，如果 $u$ 没有左子节点，则 $l_u = 0$，如果 $u$ 没有右子节点，则 $r_u = 0$。 每个节点有一个字符串标签，初始时为单个字符 $c_u$。我们定义该二叉树的字符串表示为中序遍历下所有节点标签的拼接。形式化地，设 $f(u)$ 表示以节点 $u$ 为根的子树的字符串表示，则 $f(u)$ 定义如下： $$ f(u) = \begin{cases} \texttt{}, & \text{如果 }u = 0; \\ f(l_u) + c_u + f(r_u) & \text{否则}, \end{cases} $$ 其中 $+$ 表示字符串拼接操作。 因此，整棵树的字符串表示为 $f(1)$。 对于每个节点，我们可以**至多对其标签进行一次复制**，即将 $c_u$ 赋值为 $c_u + c_u$，但只有当 $u$ 是树的根节点，或者其父节点的标签也已经被复制时，才允许对 $u$ 进行复制。 给定这棵树和一个整数 $k$。如果最多可以对 $k$ 个节点的标签进行复制，求该树的字典序最小的字符串表示。 如果字符串 $a$ 是字符串 $b$ 的前缀且 $a \ne b$，则 $a$ 字典序小于 $b$；或者在第一个不同的位置，$a$ 的字母在字母表中比 $b$ 的对应字母更靠前，则 $a$ 字典序小于 $b$。

第一行包含两个整数 $n$ 和 $k$（$1 \le k \le n \le 2 \cdot 10^5$）。 第二行包含一个长度为 $n$ 的小写英文字母字符串 $c$，其中 $c_i$ 是节点 $i$ 的初始标签。注意，给定的字符串 $c$ **不是**树的初始字符串表示。 接下来的 $n$ 行，每行包含两个整数 $l_i$ 和 $r_i$（$0 \le l_i, r_i \le n$）。如果节点 $i$ 没有左子节点，则 $l_i = 0$，如果没有右子节点，则 $r_i = 0$。 保证输入数据构成一棵以 $1$ 号节点为根的二叉树。

输出一行，表示在最多对 $k$ 个节点的标签进行复制的情况下，树的字典序最小的字符串表示。

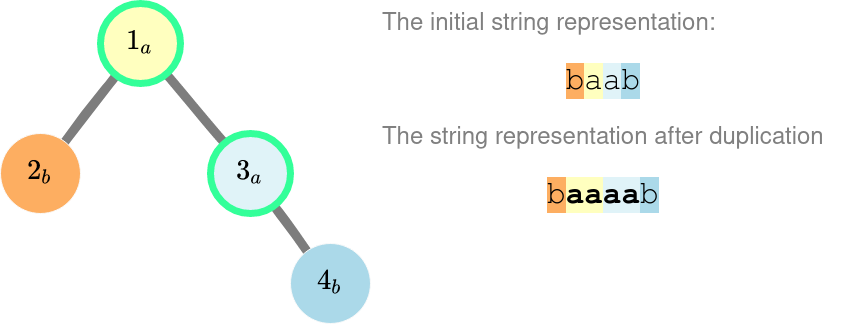
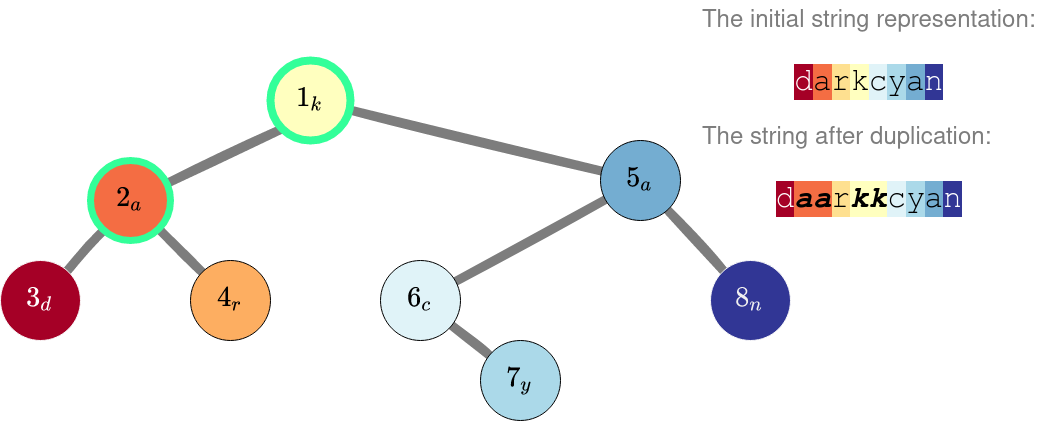
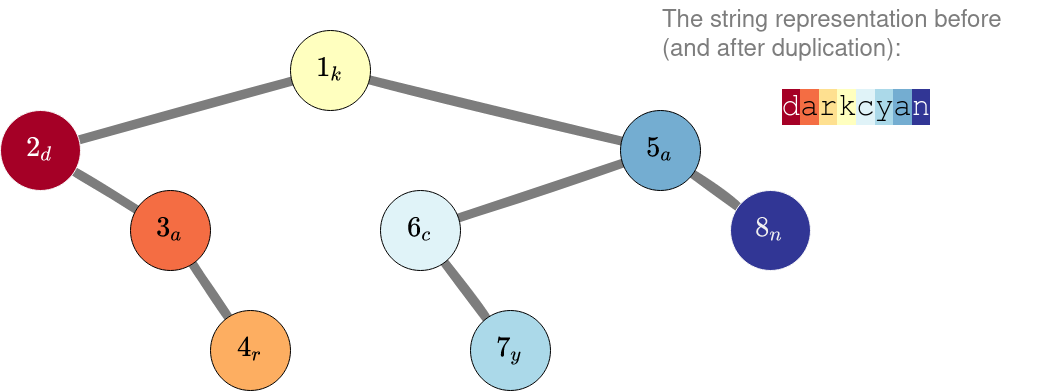
下图展示了样例的树结构。每个节点中的数字为节点编号，下标字母为其标签。右侧为树的字符串表示，每个字母颜色与对应节点一致。 这是第一个样例的树。此处我们复制了节点 $1$ 和 $3$ 的标签。不应复制节点 $2$ 的标签，否则结果为 "bbaaab"，字典序大于 "baaaab"。  在第二个样例中，我们可以复制节点 $1$ 和 $2$ 的标签。注意，仅复制根节点的标签会得到比初始字符串更差的结果。  在第三个样例中，不应复制任何字符。即使我们想复制节点 $3$ 的标签，但复制它时必须也复制节点 $2$ 的标签，这会导致更差的结果。  无法通过复制操作将初始字符串 "darkcyan" 变为 "darkkcyan"。 由 ChatGPT 4.1 翻译