CF1624G MinOr Tree

最近，Vlad 对生成树产生了浓厚的兴趣，因此他的朋友们毫不犹豫地送给他一个有 $n$ 个顶点和 $m$ 条边的连通带权无向图作为生日礼物。 Vlad 定义一棵生成树的 ority 为其所有边权的按位或（bitwise OR），现在他想知道，通过选择某棵生成树，能够得到的最小 ority 是多少。生成树是给定图的一个连通且无环的子图。 换句话说，你需要保留 $n-1$ 条边，使得图仍然连通，并且这些边的权值的按位或尽可能小。你需要求出最小的按位或值。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例前有一个空行。 接下来一行包含两个整数 $n$ 和 $m$（$3 \le n \le 2 \cdot 10^5,\, n-1 \le m \le 2 \cdot 10^5$），分别表示图的顶点数和边数。 接下来的 $m$ 行，每行包含三个整数 $v_i$、$u_i$ 和 $w_i$（$1 \le v_i, u_i \le n$，$1 \le w_i \le 10^9$，$v_i \neq u_i$），表示一条连接顶点 $v_i$ 和 $u_i$ 的边及其权值。 保证所有测试用例中 $m$ 的总和与 $n$ 的总和均不超过 $2 \cdot 10^5$，且每个测试用例中的图都是连通的。

输出 $t$ 行，每行一个整数，表示对应测试用例的最小生成树 ority。

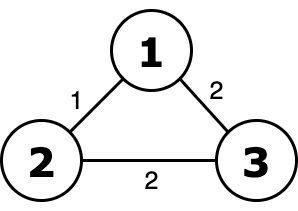 第一组数据的图。 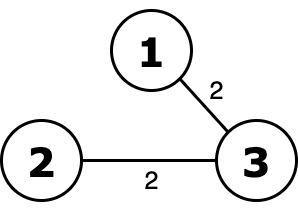 这棵树的 ority 等于 $2 \,\mathrm{or}\, 2 = 2$，且是最小的。 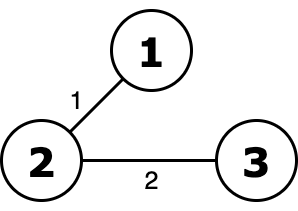 如果不去掉权值为 $1$ 的边，ority 就是 $1\,\mathrm{or}\, 2 = 3$。 由 ChatGPT 4.1 翻译