CF1625B Elementary Particles

火星人正在积极参与星际贸易。以其太空港闻名的奥林匹斯城，已经成为银河系各地货物的集散地。为了从遥远的星球运送更多的货物，火星人需要更快的飞船。 一组科学家正在进行实验，以制造新飞船的高速引擎。在当前的实验中，有 $n$ 个基本粒子，第 $i$ 个粒子的类型为 $a_i$。 我们将粒子序列 $(a_1, a_2, \dots, a_n)$ 的一个子区间定义为 $(a_l, a_{l+1}, \dots, a_r)$，其中左端点 $l$ 和右端点 $r$ 满足 $1 \le l \le r \le n$。例如，序列 $(1\ 4\ 2\ 8\ 5\ 7)$ 中，$l=2$ 且 $r=4$ 时，子区间为 $(4\ 2\ 8)$。如果两个子区间的端点至少有一个不同，则认为它们是不同的子区间。 注意，即使两个子区间作为序列完全相同，只要它们的端点不同，也被视为不同。例如，序列 $(1\ 1\ 1\ 1\ 1)$ 的两个子区间：一个 $l=1, r=3$，另一个 $l=2, r=4$，它们都是 $(1\ 1\ 1)$，但由于端点不同，仍然被视为不同的子区间。 科学家们希望进行一次反应，得到两个长度相同但不同的子区间。记这个长度为 $k$。这对子区间必须是“和谐的”，即存在某个 $i$（$1 \le i \le k$），使得这两个子区间在第 $i$ 个位置上的粒子类型相同。例如，$(1\ 7\ 3)$ 和 $(4\ 7\ 8)$ 是和谐的，因为它们在第二个位置上都是 $7$。而 $(1\ 2\ 3)$ 和 $(3\ 1\ 2)$ 则不是和谐的。 和谐子区间的长度越长，科学家们制造出高速引擎的机会就越大。因此，他们希望你计算由不同子区间组成的和谐对子区间的最大可能长度。

第一行包含一个整数 $t$（$1 \le t \le 100$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$2 \le n \le 150\,000$），表示粒子序列的长度。 第二行包含 $n$ 个整数 $a_i$（$1 \le a_i \le 150\,000$），表示每个粒子的类型。 保证所有测试用例的 $n$ 之和不超过 $3 \times 10^5$。

对于每个测试用例，输出一个整数，表示由不同子区间组成的和谐对子区间的最大可能长度。如果不存在这样的对子区间，输出 $-1$。

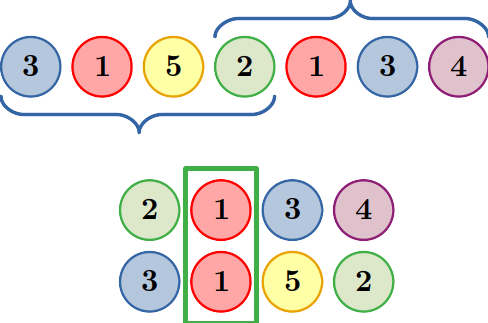
第一个测试用例如下图所示：  如图所示，你可以选择子区间 $(2\ 1\ 3\ 4)$ 和 $(3\ 1\ 5\ 2)$，它们是一对和谐对子区间。它们的长度为 $4$，所以答案是 $4$。 在第二个测试用例中，你需要选择两个子区间：一个 $l=1, r=5$，另一个 $l=2, r=6$。可以发现这两个区间是一对和谐对子区间，并且由于端点不同，视为不同的子区间，尽管它们的内容完全相同。 在第三个测试用例中，无法构成和谐对子区间，因此答案为 $-1$。 由 ChatGPT 4.1 翻译