CF1625C Road Optimization

火星政府不仅致力于优化太空飞行，还希望改善该星球的公路系统。 火星最重要的高速公路之一连接着奥林匹城和 Cydonia 的首都 Kstolop。在本题中，我们只考虑从 Kstolop 到奥林匹城的路线，不考虑反向（即从奥林匹城到 Kstolop 的路线）。 从 Kstolop 到奥林匹城的公路长为 $\ell$ 公里。公路上的每个点都有一个坐标 $x$（$0 \le x \le \ell$），表示该点距离 Kstolop 的距离（单位为公里）。因此，Kstolop 位于坐标为 $0$ 的点，奥林匹城位于坐标为 $\ell$ 的点。 公路上有 $n$ 个限速标志，第 $i$ 个标志规定了限速 $a_i$。这个限速意味着接下来的每一公里都需要用 $a_i$ 分钟通过，直到遇到下一个限速标志为止。公路起点（即坐标为 $0$ 的点）有一个限速标志，规定了初始限速。 如果你知道所有标志的位置，计算从 Kstolop 到奥林匹城所需的时间并不难。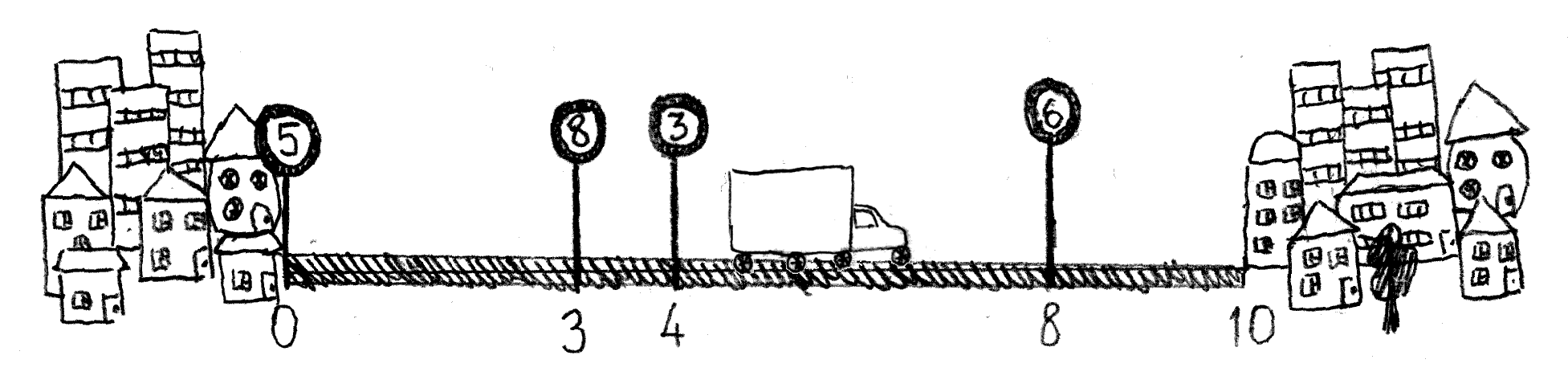举例如下：  在这个例子中，你需要用每公里 5 分钟的速度行驶前三公里，然后用 8 分钟行驶一公里，接着用每公里 3 分钟的速度行驶四公里，最后用每公里 6 分钟的速度行驶最后两公里。总时间为 $3\cdot 5 + 1\cdot 8 + 4\cdot 3 + 2\cdot 6 = 47$ 分钟。 为了优化道路交通，火星政府决定最多移除 $k$ 个限速标志。起点的限速标志不能被移除，否则起点就没有限速了。通过移除这些标志，政府希望使从 Kstolop 到奥林匹城所需的时间尽可能少。 Cydonia 拥有最大的工业企业，因此优化从奥林匹城出发的道路交通是首要任务。因此，火星政府希望你按照上述方式移除标志。

第一行包含三个整数 $n$、$\ell$、$k$（$1 \le n \le 500$，$1 \le \ell \le 10^5$，$0 \le k \le n-1$），分别表示公路上的限速标志数量、两城市之间的距离以及最多可以移除的标志数量。 第二行包含 $n$ 个整数 $d_i$（$d_1 = 0$，$d_i < d_{i+1}$，$0 \le d_i \le \ell - 1$），表示所有限速标志的位置。 第三行包含 $n$ 个整数 $a_i$（$1 \le a_i \le 10^4$），表示各个限速标志规定的限速。

输出一个整数，表示在最多移除 $k$ 个限速标志的情况下，从 Kstolop 到奥林匹城所需的最小时间（单位为分钟）。

在第一个样例中，不能移除任何标志。因此答案为 $47$，如题目所述。 在第二个样例中，可以移除第 2 个和第 4 个标志。此时，你需要用 $4\cdot 5 = 20$ 分钟行驶四公里，然后用 $6\cdot 3 = 18$ 分钟行驶六公里，所以总时间为 $4\cdot 5 + 6\cdot 3 = 38$ 分钟。 由 ChatGPT 4.1 翻译