CF1627B Not Sitting

Rahul 和 Tina 期待着在大学开始新的一年。当他们走进新教室时，发现学生的座位被安排成一个 $n \times m$ 的网格。第 $r$ 行第 $c$ 列的座位记作 $(r, c)$，而两个座位 $(a, b)$ 和 $(c, d)$ 之间的距离为 $|a-c| + |b-d|$。 作为班长，Tina 恰好有 $k$ 桶粉色油漆。接下来会发生如下过程： - 首先，Tina 选择教室中的恰好 $k$ 个座位用粉色油漆涂上。一桶油漆只能涂一个座位。 - 在 Tina 涂好 $k$ 个座位后，Rahul 选择自己的座位。他不会选择被涂成粉色的座位，因为他讨厌粉色。 - 在 Rahul 选好座位后，Tina 选择自己的座位。她可以选择除 Rahul 所选座位以外的任意座位（无论是否被涂色）。 Rahul 想选择一个尽可能靠近 Tina 的座位。然而，Tina 却想尽可能远离 Rahul（由于一些复杂的历史原因，这里就不展开了）。 现在，Rahul 想知道对于 $k = 0, 1, \dots, n \cdot m - 1$，如果 Tina 有 $k$ 桶油漆，在双方都了解对方意图并且都采取最优策略的情况下，Rahul 距离 Tina 的最小可能距离是多少？请帮 Rahul 解答他的疑问！

输入包含多组测试用例。第一行包含一个整数 $t$（$1 \leq t \leq 5 \cdot 10^4$）——测试用例的数量。 每个测试用例的第一行包含两个整数 $n$、$m$（$2 \leq n \cdot m \leq 10^5$）——教室的行数和列数。 所有测试用例中 $n \cdot m$ 的总和不超过 $10^5$。

对于每个测试用例，输出 $n \cdot m$ 个有序整数——在每个 $k \in [0, n \cdot m - 1]$ 的情况下，Rahul 和 Tina 在双方都采取最优策略时的最小距离。

以下是第一个测试用例中 Tina 有 $k=3$ 桶油漆时可能的选择过程。 Tina 将 $(1, 2)$、$(2, 2)$、$(3, 2)$ 这三个座位涂成粉色。Rahul 选择 $(3, 1)$ 作为自己的座位，Tina 随后选择 $(1, 3)$ 作为自己的座位。 因此，Tina 和 Rahul 之间的距离为 $|3-1| + |1-3| = 4$，并且可以证明在给定约束下这是最小可能距离。当然，也可能有其他选择方案得到相同的答案。 对于第一个测试用例的 $k=0$，Rahul 可以选择 $(2, 2)$，Tina 可以选择 $(4, 3)$，此时他们之间的距离为 $|2-4| + |2-3| = 3$。 下图展示了第一个测试用例中 $k=3$ 和 $k=0$ 时的一种可能座位安排。 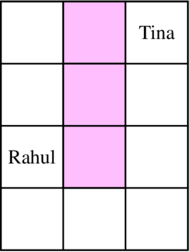 $k=3$ 时的一种可能座位安排。 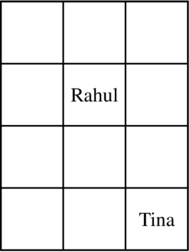 $k=0$ 时的一种可能座位安排。 由 ChatGPT 4.1 翻译