CF1627E Not Escaping

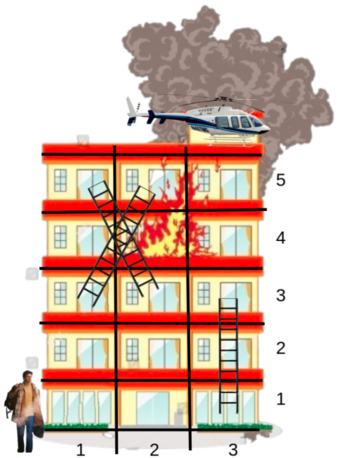
Ram 少校正被他的死敌 Raghav 追赶。Ram 必须到达大楼的顶层，才能乘直升机逃脱。然而，大楼正在燃烧。Ram 必须选择一条最优路径，以损失最少的生命值到达大楼顶层。 大楼共有 $n$ 层，每层有 $m$ 个房间。用 $(i, j)$ 表示第 $i$ 层的第 $j$ 个房间。此外，大楼中安装了 $k$ 个梯子。第 $i$ 个梯子允许 Ram 从 $(a_i, b_i)$ 到 $(c_i, d_i)$，但不能反向使用。Ram 使用第 $i$ 个梯子时会获得 $h_i$ 点生命值。保证所有梯子都有 $a_i < c_i$。 如果 Ram 在第 $i$ 层，他可以向左或向右移动。在同一层内，从 $(i, j)$ 移动到 $(i, k)$，会损失 $|j-k| \cdot x_i$ 点生命值。 Ram 从 $(1, 1)$ 进入大楼，直升机停在 $(n, m)$ 等待他。请问 Ram 选择最优路径后，最少会损失多少生命值？注意，答案可能为负数（即他获得了生命值）。如果无论如何都无法逃脱，请输出 "NO ESCAPE"。 

输入的第一行包含一个整数 $t$（$1 \leq t \leq 5 \cdot 10^4$），表示测试用例的数量。 每个测试用例的第一行包含三个整数 $n, m, k$（$2 \leq n, m \leq 10^5$；$1 \leq k \leq 10^5$），分别表示楼层数、每层房间数和梯子的数量。 每个测试用例的第二行包含 $n$ 个整数 $x_1, x_2, \dots, x_n$（$1 \leq x_i \leq 10^6$）。 接下来的 $k$ 行描述每个梯子。第 $i$ 个梯子用 $a_i, b_i, c_i, d_i, h_i$ 表示（$1 \leq a_i < c_i \leq n$；$1 \leq b_i, d_i \leq m$；$1 \leq h_i \leq 10^6$），表示梯子连接的房间和使用该梯子获得的生命值。 保证所有梯子都有 $a_i < c_i$，且任意两房间之间至多有一条梯子。 所有测试用例中 $n$、$m$、$k$ 的总和不超过 $10^5$。

对于每个测试用例，输出从 $(1, 1)$ 到 $(n, m)$ 的最小生命值损失。如果无论如何都无法逃脱，请输出 "NO ESCAPE"（全部大写，不带引号）。

第一个测试用例的图见题面。到 $(n, m)$ 只有两条可能的路径： - Ram 先到 $(1, 3)$，使用梯子到 $(3, 3)$，再到 $(3, 2)$，使用梯子到 $(5, 1)$，最后到 $(5, 3)$ 乘直升机逃脱。生命值损失为 $$ \begin{aligned} &\mathrel{\phantom{=}} x_1 \cdot |1-3| - h_1 + x_3 \cdot |3-2| - h_3 + x_5 \cdot |1-3| \\ &= 5 \cdot 2 - 4 + 8 \cdot 1 - 6 + 4 \cdot 2 \\ &= 16。 \end{aligned} $$ - Ram 先到 $(1, 3)$，使用梯子到 $(3, 3)$，再到 $(3, 1)$，使用梯子到 $(5, 2)$，最后到 $(5, 3)$ 乘直升机逃脱。生命值损失为 $$ \begin{aligned} &\mathrel{\phantom{=}} x_1 \cdot |1-3| - h_1 + x_3 \cdot |3-1| - h_2 + x_5 \cdot |2-3| \\ &= 5 \cdot 2 - 4 + 8 \cdot 2 - 5 + 4 \cdot 1 \\ &= 21。 \end{aligned} $$ 因此，最小生命值损失为 $16$。 第二个测试用例中，没有路径可以到达 $(n, m)$。 第三个测试用例中，Ram 先到 $(1, 3)$，使用唯一的梯子到 $(5, 3)$。他损失 $5 \cdot 2$ 生命值，获得 $h_1 = 100$ 生命值。因此总损失为 $10-100=-90$（负数表示他获得了生命值）。 由 ChatGPT 4.1 翻译