CF1628F Spaceship Crisis Management

NASA（挪威宇航员装备协会）正在为宇宙飞船开发一套新的导航系统。但目前的系统还不够安全，因为飞船有可能会撞上太空垃圾。为了让导航系统更加安全，他们需要解决如下问题： 给定目标位置 $t = (0, 0)$，以及 $n$ 个太空垃圾，每个垃圾用线段 $l_i = ((a_{ix}, a_{iy}), (b_{ix}, b_{iy}))$ 描述，还有一个起始位置 $s = (s_x, s_y)$，请判断是否存在一个方向，使得从起始位置沿该方向漂浮，最终能够到达目标位置？ 当飞船撞上太空垃圾时，根据漂浮方向与该线段的夹角的绝对值 $\theta$，会发生以下情况： - 如果 $\theta < 45^{\circ}$，飞船会沿着太空垃圾滑行，滑行方向选择使得角度变化最小的方向。当飞船滑出垃圾线段末端时，会继续以撞击前的原方向漂浮。 - 如果 $\theta \ge 45^{\circ}$，飞船会停止，因为摩擦力太大，无法沿垃圾滑行。 你只会获得一次所有太空垃圾的信息，目标位置始终为 $(0, 0)$，但有 $q$ 个询问，每次询问给出一个起始位置 $s_j = (s_{jx}, s_{jy})$。 请你对于每个询问，回答上述问题。

第一行包含一个整数 $n$（$1 \le n \le 1500$）。 接下来 $n$ 行，每行包含 $4$ 个整数 $a_{ix}$、$a_{iy}$、$b_{ix}$、$b_{iy}$（$|a_{ix}|, |a_{iy}|, |b_{ix}|, |b_{iy}| \le 1000$），表示第 $i$ 个太空垃圾的两个端点。 接下来一行包含一个整数 $q$（$1 \le q \le 1000$）。 接下来 $q$ 行，每行包含 $2$ 个整数 $s_{jx}$ 和 $s_{jy}$（$|s_{jx}|, |s_{jy}| \le 1000$），表示第 $j$ 个询问的起始位置。 保证所有垃圾线段两两不相交也不相切，目标点 $t$ 不在任何垃圾线段上，所有起始点 $s_j$ 也不在任何垃圾线段上，且 $s \neq t$。

对于每个询问 $s_j$，输出一行答案。如果存在某个方向，使得从 $s_j$ 沿该方向漂浮（可能会沿垃圾滑行），最终能到达 $t$，则输出 "YES"；否则输出 "NO"（不区分大小写）。

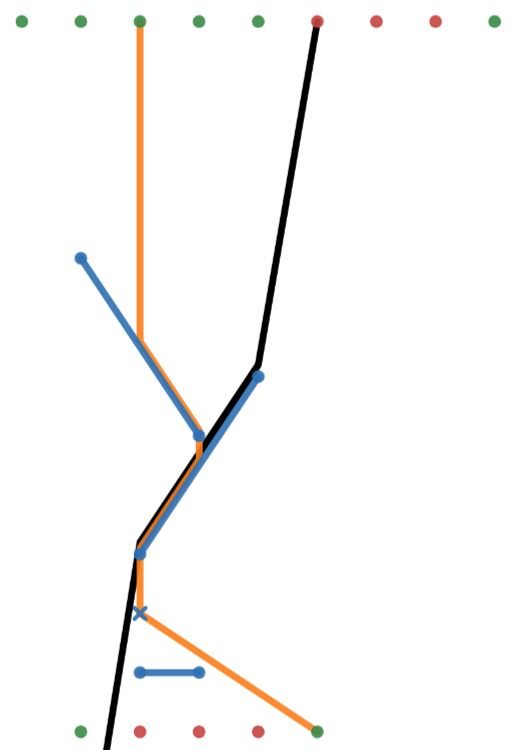
 蓝色的叉号表示目标位置，其他蓝色线段表示太空垃圾。 绿色点表示起点可以到达目标点（答案为 YES），红色点表示不能到达（答案为 NO）。 黄色线表示第 $3$ 个和第 $14$ 个询问的可能路径。 黑色线表示第 $6$ 个询问的起点的某条可能路径，但它恰好错过了目标点。 由 ChatGPT 4.1 翻译