CF1630C Paint the Middle

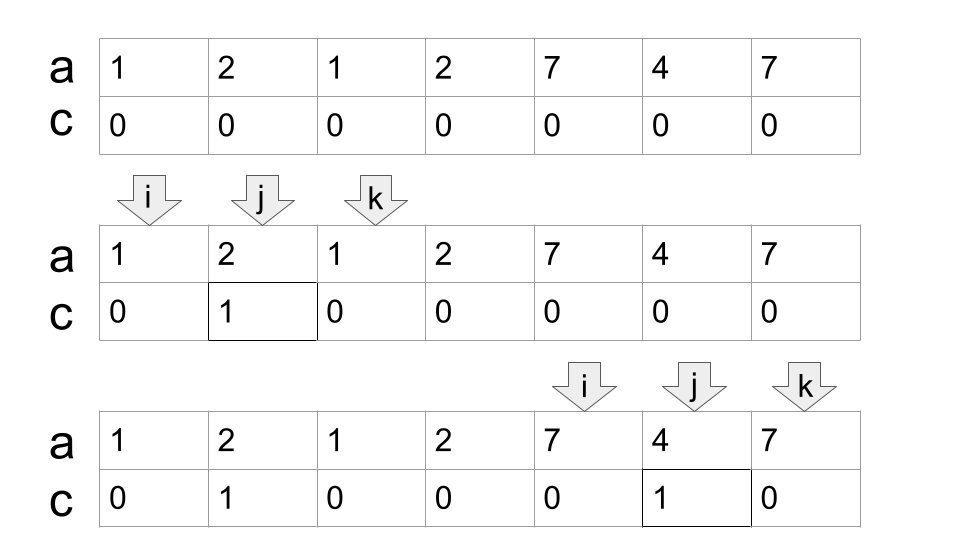
You are given $ n $ elements numbered from $ 1 $ to $ n $ , the element $ i $ has value $ a_i $ and color $ c_i $ , initially, $ c_i = 0 $ for all $ i $ . The following operation can be applied: - Select three elements $ i $ , $ j $ and $ k $ ( $ 1 \leq i < j < k \leq n $ ), such that $ c_i $ , $ c_j $ and $ c_k $ are all equal to $ 0 $ and $ a_i = a_k $ , then set $ c_j = 1 $ . Find the maximum value of $ \sum\limits_{i=1}^n{c_i} $ that can be obtained after applying the given operation any number of times.

The first line contains an integer $ n $ ( $ 3 \leq n \leq 2 \cdot 10^5 $ ) — the number of elements. The second line consists of $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ 1 \leq a_i \leq n $ ), where $ a_i $ is the value of the $ i $ -th element.

Print a single integer in a line — the maximum value of $ \sum\limits_{i=1}^n{c_i} $ that can be obtained after applying the given operation any number of times.

In the first test, it is possible to apply the following operations in order: