CF1630F Making It Bipartite

You are given an undirected graph of $ n $ vertices indexed from $ 1 $ to $ n $ , where vertex $ i $ has a value $ a_i $ assigned to it and all values $ a_i $ are different. There is an edge between two vertices $ u $ and $ v $ if either $ a_u $ divides $ a_v $ or $ a_v $ divides $ a_u $ . Find the minimum number of vertices to remove such that the remaining graph is bipartite, when you remove a vertex you remove all the edges incident to it.

The input consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. Description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 5\cdot10^4 $ ) — the number of vertices in the graph. The second line of each test case contains $ n $ integers, the $ i $ -th of them is the value $ a_i $ ( $ 1 \le a_i \le 5\cdot10^4 $ ) assigned to the $ i $ -th vertex, all values $ a_i $ are different. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 5\cdot10^4 $ .

For each test case print a single integer — the minimum number of vertices to remove such that the remaining graph is bipartite.

In the first test case if we remove the vertices with values $ 1 $ and $ 2 $ we will obtain a bipartite graph, so the answer is $ 2 $ , it is impossible to remove less than $ 2 $ vertices and still obtain a bipartite graph. BeforeAfter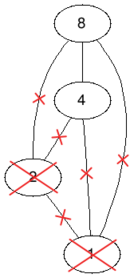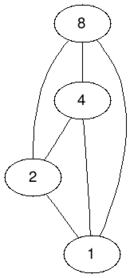test case #1In the second test case we do not have to remove any vertex because the graph is already bipartite, so the answer is $ 0 $ . BeforeAfter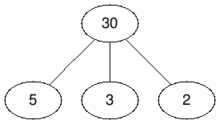test case #2In the third test case we only have to remove the vertex with value $ 12 $ , so the answer is $ 1 $ . BeforeAfter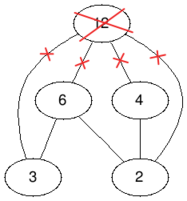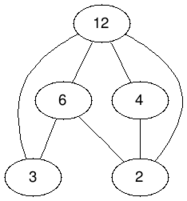test case #3In the fourth test case we remove the vertices with values $ 2 $ and $ 195 $ , so the answer is $ 2 $ . BeforeAfter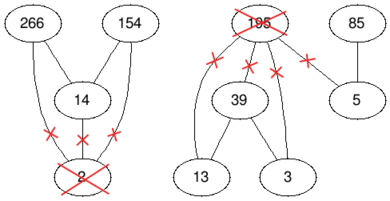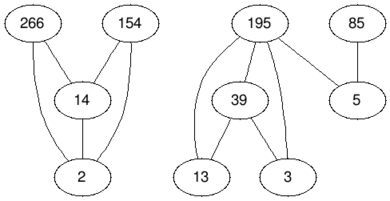test case #4