CF1632E2 Distance Tree (hard version)

This version of the problem differs from the previous one only in the constraint on $ n $ . A tree is a connected undirected graph without cycles. A weighted tree has a weight assigned to each edge. The distance between two vertices is the minimum sum of weights on the path connecting them. You are given a weighted tree with $ n $ vertices, each edge has a weight of $ 1 $ . Denote $ d(v) $ as the distance between vertex $ 1 $ and vertex $ v $ . Let $ f(x) $ be the minimum possible value of $ \max\limits_{1 \leq v \leq n} \ {d(v)} $ if you can temporarily add an edge with weight $ x $ between any two vertices $ a $ and $ b $ $ (1 \le a, b \le n) $ . Note that after this operation, the graph is no longer a tree. For each integer $ x $ from $ 1 $ to $ n $ , find $ f(x) $ .

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 3 \cdot 10^5 $ ). Each of the next $ n−1 $ lines contains two integers $ u $ and $ v $ ( $ 1 \le u,v \le n $ ) indicating that there is an edge between vertices $ u $ and $ v $ . It is guaranteed that the given edges form a tree. It is guaranteed that the sum of $ n $ over all test cases doesn't exceed $ 3 \cdot 10^5 $ .

For each test case, print $ n $ integers in a single line, $ x $ -th of which is equal to $ f(x) $ for all $ x $ from $ 1 $ to $ n $ .

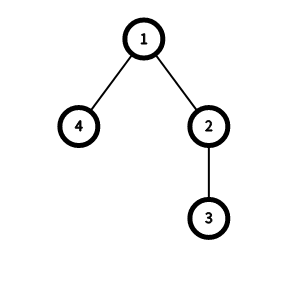 In the first testcase: - For $ x = 1 $ , we can an edge between vertices $ 1 $ and $ 3 $ , then $ d(1) = 0 $ and $ d(2) = d(3) = d(4) = 1 $ , so $ f(1) = 1 $ . - For $ x \ge 2 $ , no matter which edge we add, $ d(1) = 0 $ , $ d(2) = d(4) = 1 $ and $ d(3) = 2 $ , so $ f(x) = 2 $ .