CF1633E Spanning Tree Queries

给定一个连通的带权无向图，包含 $n$ 个顶点和 $m$ 条边。 你需要回答关于该图的 $k$ 个询问。每个询问包含一个整数 $x$。对于每个询问，你需要在图中选择一棵生成树。设其边权为 $w_1, w_2, \dots, w_{n-1}$。该生成树的代价为 $\sum\limits_{i=1}^{n-1} |w_i - x|$（即所有边权与 $x$ 的绝对差之和）。每个询问的答案是生成树的最小代价。 这些询问以压缩格式给出。前 $p$ 个（$1 \le p \le k$）询问 $q_1, q_2, \dots, q_p$ 被直接给出。对于第 $p+1$ 到第 $k$ 个询问，有 $q_j = (q_{j-1} \cdot a + b) \bmod c$。 请输出所有询问答案的异或和。

第一行包含两个整数 $n$ 和 $m$（$2 \le n \le 50$；$n-1 \le m \le 300$），表示图的顶点数和边数。 接下来的 $m$ 行，每行包含三个整数 $v$、$u$ 和 $w$（$1 \le v, u \le n$；$v \neq u$；$0 \le w \le 10^8$），表示一条无向边及其权值。注意，两个顶点之间可能有多条边。所有边构成一个连通图。 接下来一行包含五个整数 $p, k, a, b, c$（$1 \le p \le 10^5$；$p \le k \le 10^7$；$0 \le a, b \le 10^8$；$1 \le c \le 10^8$），分别表示直接给出的询问数、总询问数以及生成询问的参数。 下一行包含 $p$ 个整数 $q_1, q_2, \dots, q_p$（$0 \le q_j < c$），表示前 $p$ 个询问。

输出一个整数，表示所有询问答案的异或和。

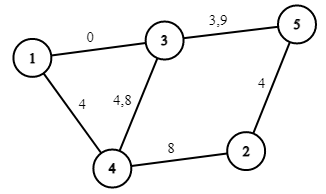
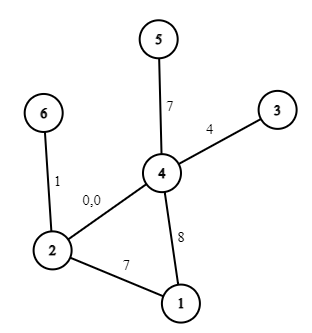
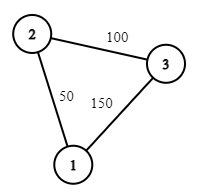
第一个样例中的询问为 $0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0$。对应的答案为 $11, 9, 7, 3, 1, 5, 8, 7, 5, 7, 11$。  第二个样例中的询问为 $3, 0, 2, 1, 6, 0, 3, 5, 4, 1$。对应的答案为 $14, 19, 15, 16, 11, 19, 14, 12, 13, 16$。  第三个样例中的询问为 $75, 0, 0, \dots$。对应的答案为 $50, 150, 150, \dots$。  由 ChatGPT 4.1 翻译