CF1638D Big Brush

You found a painting on a canvas of size $ n \times m $ . The canvas can be represented as a grid with $ n $ rows and $ m $ columns. Each cell has some color. Cell $ (i, j) $ has color $ c_{i,j} $ . Near the painting you also found a brush in the shape of a $ 2 \times 2 $ square, so the canvas was surely painted in the following way: initially, no cell was painted. Then, the following painting operation has been performed some number of times: - Choose two integers $ i $ and $ j $ ( $ 1 \le i < n $ , $ 1 \le j < m $ ) and some color $ k $ ( $ 1 \le k \le nm $ ). - Paint cells $ (i, j) $ , $ (i + 1, j) $ , $ (i, j + 1) $ , $ (i + 1, j + 1) $ in color $ k $ . All cells must be painted at least once. A cell can be painted multiple times. In this case, its final color will be the last one. Find any sequence of at most $ nm $ operations that could have led to the painting you found or state that it's impossible.

The first line of input contains two integers $ n $ and $ m $ ( $ 2 \le n, m \le 1000 $ ) — the dimensions of the canvas. On the $ i $ -th of the next $ n $ lines of input, there will be $ m $ integers. The $ j $ -th of them is $ a_{i,j} $ ( $ 1 \le a_{i,j} \le nm $ ) — the color of cell $ (i, j) $ .

If there is no solution, print a single integer $ -1 $ . Otherwise, on the first line, print one integer $ q $ ( $ 1 \le q \le nm $ ) — the number of operations. Next, print the operations in order. On the $ k $ -th of the next $ q $ lines, print three integers $ i $ , $ j $ , $ c $ ( $ 1 \le i < n $ , $ 1 \le j < m $ , $ 1 \le c \le nm $ ) — the description of the $ k $ -th operation. If there are multiple solutions, print any.

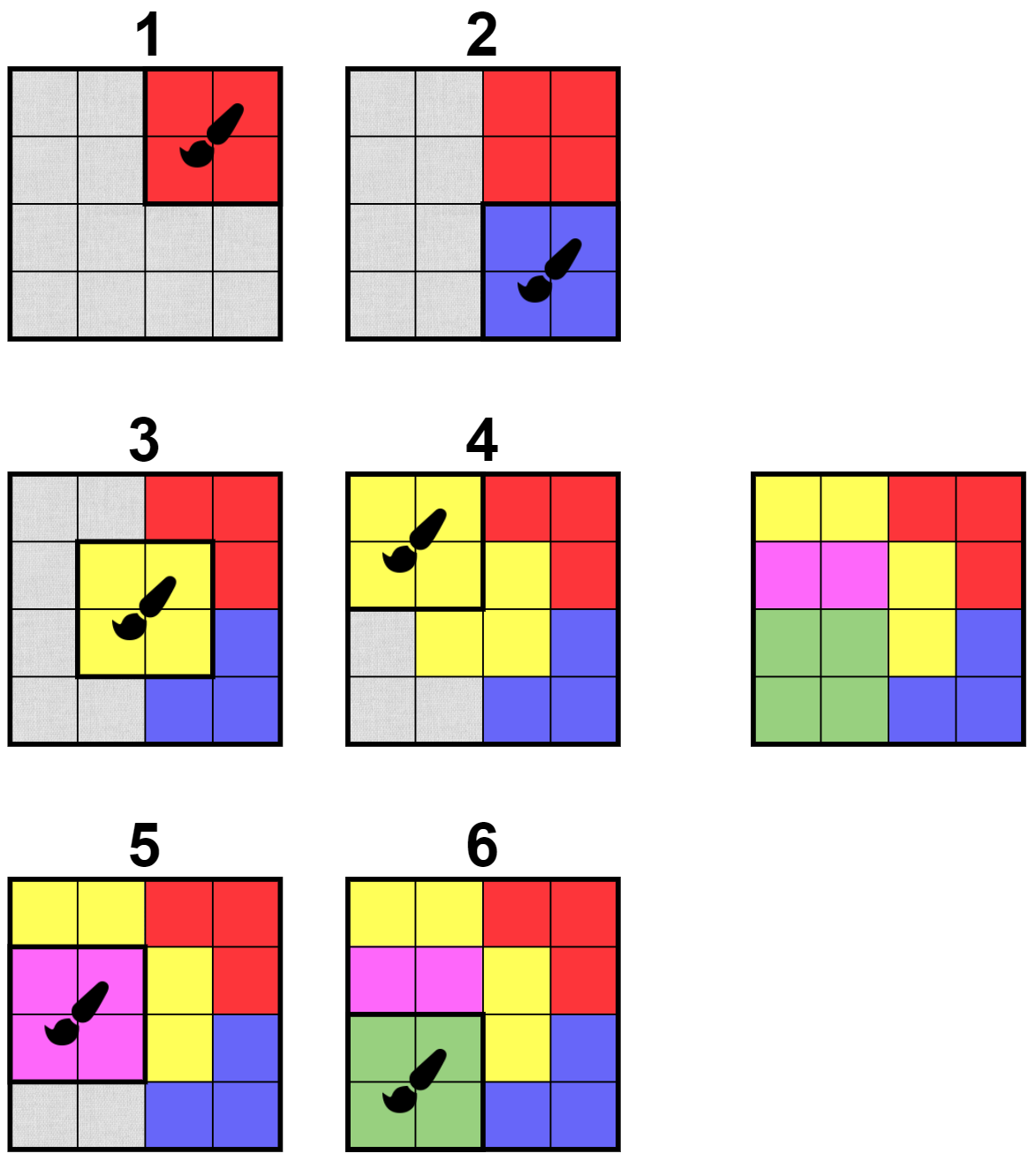In the first test case, the solution is not unique. Here's one of them: In the second test case, there is no way one could obtain the given painting, thus the answer is $ -1 $ .