CF1638D Big Brush

你发现了一幅画，这幅画画在一个 $n \times m$ 的画布上。这个画布可以用一个有 $n$ 行 $m$ 列的网格表示，每个格子都有一种颜色。第 $(i, j)$ 个格子的颜色为 $c_{i,j}$。 在画作旁边，你还发现了一把形状为 $2 \times 2$ 的刷子，因此这幅画一定是通过如下方式绘制的：最开始，所有格子都没有被涂色。然后，进行了若干次如下的涂色操作： - 选择两个整数 $i$ 和 $j$（$1 \le i < n$，$1 \le j < m$）以及某种颜色 $k$（$1 \le k \le nm$）。 - 用颜色 $k$ 涂色 $(i, j)$、$(i + 1, j)$、$(i, j + 1)$、$(i + 1, j + 1)$ 这四个格子。 所有格子都必须至少被涂色一次。一个格子可以被多次涂色，这种情况下，它的最终颜色为最后一次涂色的颜色。 请你找出最多 $nm$ 次操作的一种方案，使得最终画布的颜色与给定的画布一致，或者判断是否不可能实现。

输入的第一行包含两个整数 $n$ 和 $m$（$2 \le n, m \le 1000$），表示画布的尺寸。 接下来的 $n$ 行，每行 $m$ 个整数，第 $i$ 行第 $j$ 个数为 $a_{i,j}$（$1 \le a_{i,j} \le nm$），表示第 $(i, j)$ 个格子的颜色。

如果不存在可行方案，输出一个整数 $-1$。 否则，第一行输出一个整数 $q$（$1 \le q \le nm$），表示操作次数。 接下来 $q$ 行，每行三个整数 $i$、$j$、$c$（$1 \le i < n$，$1 \le j < m$，$1 \le c \le nm$），表示第 $k$ 次操作的描述。 如果有多种方案，输出任意一种即可。

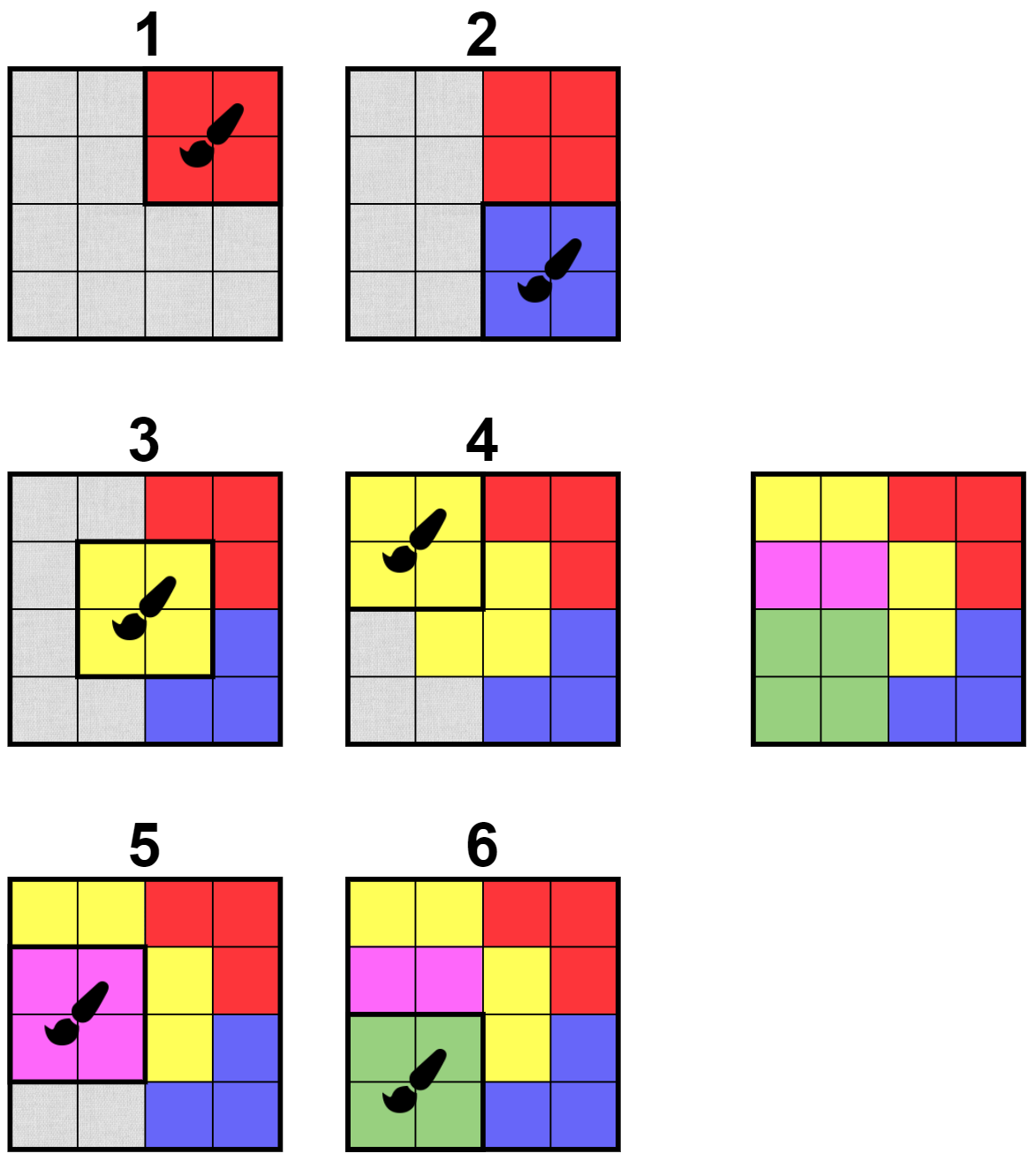
在第一个样例中，方案不唯一。以下是其中一种：  在第二个样例中，不存在任何方案可以得到给定的画布，因此输出 $-1$。 由 ChatGPT 4.1 翻译