CF163B Lemmings

As you know, lemmings like jumping. For the next spectacular group jump $ n $ lemmings gathered near a high rock with $ k $ comfortable ledges on it. The first ledge is situated at the height of $ h $ meters, the second one is at the height of $ 2h $ meters, and so on (the $ i $ -th ledge is at the height of $ i·h $ meters). The lemmings are going to jump at sunset, and there's not much time left. Each lemming is characterized by its climbing speed of $ v_{i} $ meters per minute and its weight $ m_{i} $ . This means that the $ i $ -th lemming can climb to the $ j $ -th ledge in 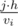 minutes. To make the jump beautiful, heavier lemmings should jump from higher ledges: if a lemming of weight $ m_{i} $ jumps from ledge $ i $ , and a lemming of weight $ m_{j} $ jumps from ledge $ j $ (for $ i

The first line contains space-separated integers $ n $ , $ k $ and $ h $ ( $ 1

Print $ k $ different numbers from $ 1 $ to $ n $ — the numbers of the lemmings who go to ledges at heights $ h,2h,...,kh $ , correspondingly, if the jump is organized in an optimal way. If there are multiple ways to select the lemmings, pick any of them.

Let's consider the first sample case. The fifth lemming (speed 10) gets to the ledge at height 2 in  minutes; the second lemming (speed 2) gets to the ledge at height 4 in 2 minutes; the fourth lemming (speed 2) gets to the ledge at height 6 in 3 minutes. All lemmings manage to occupy their positions in 3 minutes.