CF1644E Expand the Path

考虑一个 $n \times n$ 的网格。行从上到下编号为 $1$ 到 $n$，列从左到右编号为 $1$ 到 $n$。 机器人初始位于单元格 $(1, 1)$。它可以执行两种移动： - D — 向下移动一格； - R — 向右移动一格。 机器人不允许移动到网格外。 给定一个移动序列 $s$，即机器人的初始路径。该路径不会导致机器人移出网格。 你可以对该路径进行任意次数的修改（也可以不修改）。每次修改，你可以将序列中的某一个移动复制一次。也就是说，可以将某个 D 替换为 DD，或者将某个 R 替换为 RR。 请计算有多少个单元格，存在至少一种修改后的路径，使得机器人在不移出网格的前提下访问到该单元格。

第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$2 \le n \le 10^8$），表示网格的行数和列数。 每个测试用例的第二行包含一个非空字符串 $s$，仅由字符 D 和 R 组成，表示机器人的初始路径。该路径不会导致机器人移出网格。 所有测试用例中字符串 $s$ 的总长度不超过 $2 \times 10^5$。

对于每个测试用例，输出一个整数，表示存在至少一种修改后的路径，使得机器人访问到该单元格且不移出网格的单元格数量。

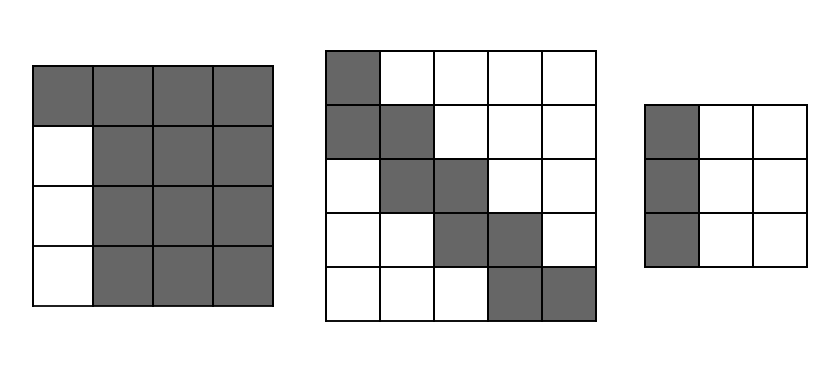
在第一个测试用例中，可以考虑如下的修改路径： - RD $\rightarrow$ RRD $\rightarrow$ RRRD $\rightarrow$ RRRDD $\rightarrow$ RRRDDD —— 该路径访问的单元格为 $(1, 1)$、$(1, 2)$、$(1, 3)$、$(1, 4)$、$(2, 4)$、$(3, 4)$ 和 $(4, 4)$； - RD $\rightarrow$ RRD $\rightarrow$ RRDD $\rightarrow$ RRDDD —— 该路径访问的单元格为 $(1, 1)$、$(1, 2)$、$(1, 3)$、$(2, 3)$、$(3, 3)$ 和 $(4, 3)$； - RD $\rightarrow$ RDD $\rightarrow$ RDDD —— 该路径访问的单元格为 $(1, 1)$、$(1, 2)$、$(2, 2)$、$(3, 2)$ 和 $(4, 2)$。 因此，至少在一条修改后的路径上被访问到的单元格有：$(1, 1)$、$(1, 2)$、$(1, 3)$、$(1, 4)$、$(2, 2)$、$(2, 3)$、$(2, 4)$、$(3, 2)$、$(3, 3)$、$(3, 4)$、$(4, 2)$、$(4, 3)$ 和 $(4, 4)$。 在第二个测试用例中，没有办法修改序列而不让机器人移出网格。因此，只有原路径上访问到的单元格会被访问。 在第三个测试用例中，至少在一条修改后的路径上被访问到的单元格有：$(1, 1)$、$(2, 1)$ 和 $(3, 1)$。 以下是所有测试用例的单元格示意图：  由 ChatGPT 4.1 翻译