CF1646D Weight the Tree

给定一棵有 $n$ 个顶点的树，顶点编号为 $1$ 到 $n$。树是一个无环连通无向图。 对于每个 $i=1,2,\ldots,n$，设 $w_i$ 为第 $i$ 个顶点的权值。如果某个顶点的权值等于其所有相邻顶点权值之和，则称该顶点为“好顶点”。 初始时所有顶点的权值未被分配。请为树中的每个顶点分配一个正整数权值，使得树中“好顶点”的数量最大。如果有多种分配方式，请找到权值和最小的一种。

第一行包含一个整数 $n$（$2\le n\le 2\cdot 10^5$），表示树的顶点数。 接下来 $n-1$ 行，每行包含两个整数 $u$ 和 $v$（$1\le u,v\le n$），表示顶点 $u$ 和顶点 $v$ 之间有一条边。保证这些边构成一棵树。

第一行输出两个整数，分别表示“好顶点”的最大数量以及在此基础上所有顶点权值和的最小值。 第二行输出 $n$ 个整数 $w_1,w_2,\ldots,w_n$（$1\le w_i\le 10^9$），表示为每个顶点分配的权值。可以证明一定存在满足条件的最优解。 如果有多种最优解，可以输出任意一种。

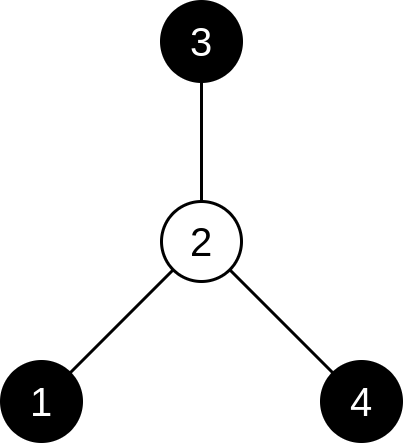
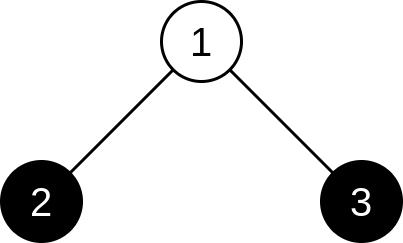
以下是第一个测试用例对应的树结构：  在这种情况下，如果给每个顶点都分配权值 $1$，则“好顶点”（黑色标记的顶点）为 $1$、$3$ 和 $4$。无法分配权值使得所有顶点都是“好顶点”。此时权值和为 $1+1+1+1=4$，且无法更小，因为权值必须为正整数。 以下是第二个测试用例对应的树结构：  在这种情况下，如果给每个顶点都分配权值 $1$，则“好顶点”（黑色标记的顶点）为 $2$ 和 $3$。可以证明这是最优分配方式。 由 ChatGPT 4.1 翻译