CF1646E Power Board
题目描述
你有一个大小为 $n\times m$ 的矩形棋盘($n$ 行 $m$ 列)。$n$ 行从上到下编号为 $1$ 到 $n$,$m$ 列从左到右编号为 $1$ 到 $m$。
第 $i$ 行第 $j$ 列的格子中写着数字 $i^j$(即 $i$ 的 $j$ 次幂)。例如,当 $n=3$,$m=3$ 时,棋盘如下所示:
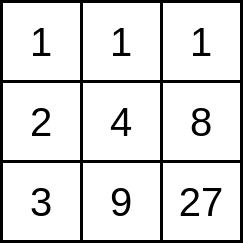
请你求出棋盘上有多少个不同的整数。
输入格式
一行包含两个整数 $n$ 和 $m$($1\le n,m\le 10^6$),分别表示棋盘的行数和列数。
输出格式
输出一个整数,表示棋盘上不同整数的个数。
说明/提示
题目描述中展示了第一个测试用例的棋盘。在这种情况下,有 $7$ 个不同的整数:$1$、$2$、$3$、$4$、$8$、$9$ 和 $27$。
在第二个测试用例中,棋盘如下:

有 $5$ 个不同的数:$1$、$2$、$4$、$8$ 和 $16$。
在第三个测试用例中,棋盘如下:

有 $6$ 个不同的数:$1$、$2$、$3$、$4$、$9$ 和 $16$。
由 ChatGPT 4.1 翻译