CF1646E Power Board

You have a rectangular board of size $ n\times m $ ( $ n $ rows, $ m $ columns). The $ n $ rows are numbered from $ 1 $ to $ n $ from top to bottom, and the $ m $ columns are numbered from $ 1 $ to $ m $ from left to right. The cell at the intersection of row $ i $ and column $ j $ contains the number $ i^j $ ( $ i $ raised to the power of $ j $ ). 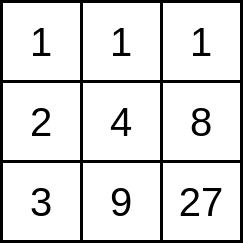For example, if $ n=3 $ and $ m=3 $ the board is as follows: Find the number of distinct integers written on the board.

The only line contains two integers $ n $ and $ m $ ( $ 1\le n,m\le 10^6 $ ) — the number of rows and columns of the board.

Print one integer, the number of distinct integers on the board.

The statement shows the board for the first test case. In this case there are $ 7 $ distinct integers: $ 1 $ , $ 2 $ , $ 3 $ , $ 4 $ , $ 8 $ , $ 9 $ , and $ 27 $ . In the second test case, the board is as follows: There are $ 5 $ distinct numbers: $ 1 $ , $ 2 $ , $ 4 $ , $ 8 $ and $ 16 $ . In the third test case, the board is as follows: There are $ 6 $ distinct numbers: $ 1 $ , $ 2 $ , $ 3 $ , $ 4 $ , $ 9 $ and $ 16 $ .