CF1659E AND-MEX Walk

有一个无向连通图，包含 $n$ 个顶点和 $m$ 条带权边。从顶点 $u$ 到顶点 $v$ 的一条“行走”定义为一个顶点序列 $p_1,p_2,\ldots,p_k$（顶点可以重复），以 $u$ 开头、以 $v$ 结尾，且对于 $1 \leq i < k$，$p_i$ 和 $p_{i+1}$ 之间有一条边相连。 我们这样定义一条行走的长度：依次记录经过的边的权值，形成一个数组。然后，对该数组的每一个非空前缀，计算其所有元素的按位与（bitwise AND），将所有结果组成一个集合。该行走的长度即为这个集合的 MEX（最小未出现的非负整数）。 更正式地，设 $[w_1,w_2,\ldots,w_{k-1}]$ 表示每一对相邻顶点之间的边权，则该行走的长度为 $\mathrm{MEX}(\{w_1,\,w_1\& w_2,\,\ldots,\,w_1\& w_2\& \ldots\& w_{k-1}\})$，其中 $\&$ 表示[按位与运算](https://en.wikipedia.org/wiki/Bitwise_operation#AND)。 现在你需要处理 $q$ 个询问，每个询问形如 $u\ v$。对于每个询问，求从 $u$ 到 $v$ 的行走的最小可能长度。 MEX（minimum excluded）指的是集合中未出现的最小非负整数。例如： - $\{2,1\}$ 的 MEX 是 $0$，因为 $0$ 不在集合中。 - $\{3,1,0\}$ 的 MEX 是 $2$，因为 $0$ 和 $1$ 在集合中，但 $2$ 不在。 - $\{0,3,1,2\}$ 的 MEX 是 $4$，因为 $0$、$1$、$2$ 和 $3$ 都在集合中，但 $4$ 不在。

第一行包含两个整数 $n$ 和 $m$（$2 \leq n \leq 10^5$；$n-1 \leq m \leq \min{\left(\frac{n(n-1)}{2},10^5\right)}$）。 接下来的 $m$ 行，每行包含三个整数 $a$、$b$ 和 $w$（$1 \leq a, b \leq n$，$a \neq b$；$0 \leq w < 2^{30}$），表示在顶点 $a$ 和顶点 $b$ 之间有一条权值为 $w$ 的无向边。输入保证没有自环和重边，且图是连通的。 接下来一行包含一个整数 $q$（$1 \leq q \leq 10^5$）。 接下来的 $q$ 行，每行包含两个整数 $u$ 和 $v$（$1 \leq u, v \leq n$，$u \neq v$），表示一个询问。

对于每个询问，输出一行一个整数，表示该询问的答案。

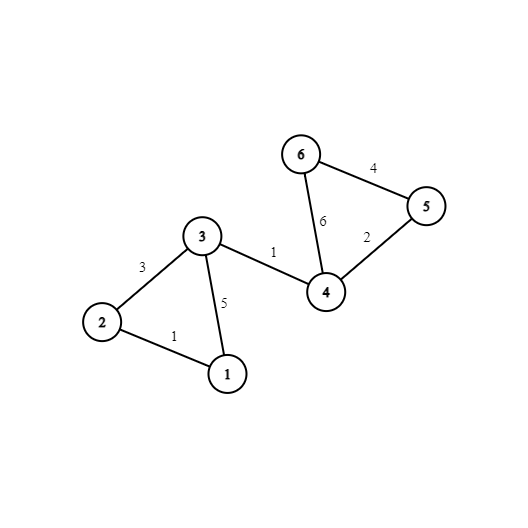
以下是第一个样例的解释。  这是第一个样例的图。对于第一个询问，有一种可能的行走如下： $1 \overset{5}{\rightarrow} 3 \overset{3}{\rightarrow} 2 \overset{1}{\rightarrow} 1 \overset{5}{\rightarrow} 3 \overset{1}{\rightarrow} 4 \overset{2}{\rightarrow} 5.$ 经过的边权数组为 $w=[5,3,1,5,1,2]$。对每个前缀做按位与，得到的集合为 $\{5,1,0\}$。该集合的 MEX 是 $2$。无法找到更短长度的行走。 由 ChatGPT 4.1 翻译