CF1660E Matrix and Shifts

给定一个 $n \times n$ 的二进制矩阵 $A$。行编号从上到下为 $1$ 到 $n$，列编号从左到右为 $1$ 到 $n$。位于第 $i$ 行第 $j$ 列的元素记作 $A_{ij}$。现有如下 $4$ 种操作： 1. 所有行循环上移一格。第 $i$ 行会被移动到第 $i-1$ 行的位置（$2 \le i \le n$），第 $1$ 行会被移动到第 $n$ 行的位置。 2. 所有行循环下移一格。第 $i$ 行会被移动到第 $i+1$ 行的位置（$1 \le i \le n-1$），第 $n$ 行会被移动到第 $1$ 行的位置。 3. 所有列循环左移一格。第 $j$ 列会被移动到第 $j-1$ 列的位置（$2 \le j \le n$），第 $1$ 列会被移动到第 $n$ 列的位置。 4. 所有列循环右移一格。第 $j$ 列会被移动到第 $j+1$ 列的位置（$1 \le j \le n-1$），第 $n$ 列会被移动到第 $1$ 列的位置。 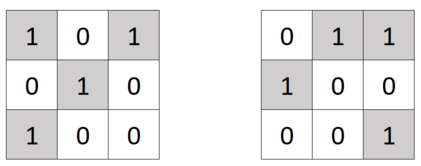 上图左侧为 $3 \times 3$ 矩阵在执行第 $3$ 种操作前的状态，右侧为执行后的状态。你可以对矩阵执行任意次（也可以不执行）上述操作，顺序不限。 之后，你可以执行任意次（也可以不执行）新的异或操作： - 选择任意一个元素 $A_{ij}$，将其赋值为 $A_{ij} \oplus 1$。也就是说，将 $(A_{ij} + 1) \bmod 2$ 写入 $A_{ij}$。 每执行一次异或操作需要花费 $1$ 个 burl。注意，前 $4$ 种循环移动操作是免费的，并且只能在执行异或操作之前进行。 请输出将矩阵 $A$ 变为单位矩阵所需支付的最小 burl 数。单位矩阵是指主对角线上的元素全为 $1$，其余元素全为 $0$（即 $A_{ij} = 1$ 当且仅当 $i = j$，否则 $A_{ij} = 0$）。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 接下来是每个测试用例的描述。每个测试用例前有一个空行。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 2000$）。 接下来有 $n$ 行，每行恰好包含 $n$ 个字符，仅由 $0$ 和 $1$ 组成，描述矩阵的元素值。 保证所有测试用例中 $n^2$ 的总和不超过 $4 \cdot 10^6$。

对于每个测试用例，输出将矩阵 $A$ 变为单位矩阵所需支付的最小 burl 数。换句话说，输出在对矩阵进行循环移动后，使其变为单位矩阵所需的最小异或操作次数。

在第一个测试用例中，你可以这样操作：首先将所有行循环下移一次，此时矩阵的主对角线全为 $1$。然后只需对唯一一个不在主对角线上的 $1$ 执行一次异或操作。 在第二个测试用例中，你可以通过将矩阵循环上移两次来得到单位矩阵。 由 ChatGPT 4.1 翻译