CF1666A Admissible Map

一张地图是一个由符号 'U'、'L'、'D' 和 'R' 组成的矩阵。 地图矩阵 $a$ 的地图图是一个有向图，包含 $n \cdot m$ 个顶点，编号为 $(i, j)$（$1 \le i \le n; 1 \le j \le m$），其中 $n$ 是矩阵的行数，$m$ 是矩阵的列数。该图有 $n \cdot m$ 条有向边 $(i, j) \to (i + di_{a_{i, j}}, j + dj_{a_{i, j}})$，其中 $(di_U, dj_U) = (-1, 0)$；$(di_L, dj_L) = (0, -1)$；$(di_D, dj_D) = (1, 0)$；$(di_R, dj_R) = (0, 1)$。当所有边都指向图中的有效顶点时，地图图是合法的。 可接受的地图是指其地图图合法且由若干个环组成的地图。 地图 $a$ 的描述是将地图的所有行依次拼接得到的字符串——即 $a_{1,1} a_{1,2} \ldots a_{1, m} a_{2, 1} \ldots a_{n, m}$。 给定一个字符串 $s$，你的任务是求有多少个 $s$ 的子串可以作为某个可接受地图的描述。 长度为 $l$ 的字符串 $s_1s_2 \ldots s_l$ 的子串由一对下标 $p$ 和 $q$（$1 \le p \le q \le l$）定义，等于 $s_ps_{p+1} \ldots s_q$。如果两对下标 $(p, q)$ 不同，即使它们表示相同的字符串，这两个子串也被认为是不同的。

输入仅一行，一个由至少一个、至多 $20\,000$ 个 'U'、'L'、'D' 或 'R' 组成的字符串 $s$。

输出一个整数，表示有多少个 $s$ 的子串可以作为某个可接受地图的描述。

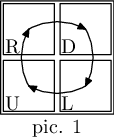
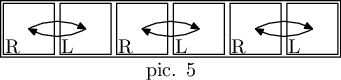
在第一个样例中，有两个子串可以作为可接受地图的描述——"RDUL" 可以作为 $2 \times 2$ 的矩阵（图 1），"DU" 可以作为 $2 \times 1$ 的矩阵（图 2）。 在第二个样例中，没有任何子串可以作为可接受地图的描述。例如，如果尝试将字符串 "RDRU" 作为 $2 \times 2$ 的矩阵，可以发现得到的图不是若干个环的集合（图 3）。 在第三个样例中，三个子串 "RL"、两个子串 "RLRL" 和一个子串 "RLRLRL" 可以作为可接受地图的描述，其中有些可以用多种方式表示。例如，子串 "RLRLRL" 可以作为 $3 \times 2$ 的矩阵（图 4）和 $1 \times 6$ 的矩阵（图 5）。      由 ChatGPT 4.1 翻译