CF1667C Half Queen Cover

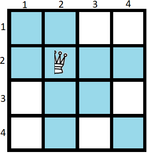You are given a board with $ n $ rows and $ n $ columns, numbered from $ 1 $ to $ n $ . The intersection of the $ a $ -th row and $ b $ -th column is denoted by $ (a, b) $ . A half-queen attacks cells in the same row, same column, and on one diagonal. More formally, a half-queen on $ (a, b) $ attacks the cell $ (c, d) $ if $ a=c $ or $ b=d $ or $ a-b=c-d $ . The blue cells are under attack. What is the minimum number of half-queens that can be placed on that board so as to ensure that each square is attacked by at least one half-queen?Construct an optimal solution.

The first line contains a single integer $ n $ ( $ 1 \le n \le 10^5 $ ) — the size of the board.

In the first line print a single integer $ k $ — the minimum number of half-queens. In each of the next $ k $ lines print two integers $ a_i $ , $ b_i $ ( $ 1 \le a_i, b_i \le n $ ) — the position of the $ i $ -th half-queen. If there are multiple solutions, print any.

Example $ 1 $ : one half-queen is enough. Note: a half-queen on $ (1, 1) $ attacks $ (1, 1) $ . Example $ 2 $ : one half-queen is enough too. $ (1, 2) $ or $ (2, 1) $ would be wrong solutions, because a half-queen on $ (1, 2) $ does not attack the cell $ (2, 1) $ and vice versa. $ (2, 2) $ is also a valid solution. Example $ 3 $ : it is impossible to cover the board with one half queen. There are multiple solutions for $ 2 $ half-queens; you can print any of them.