CF1667C Half Queen Cover

给定一个 $n$ 行 $n$ 列的棋盘，行和列编号均为 $1$ 到 $n$。第 $a$ 行第 $b$ 列的格子记作 $(a, b)$。 “半皇后”可以攻击与其处于同一行、同一列以及一条对角线上的所有格子。更正式地说，若在 $(a, b)$ 放置一枚半皇后，则其可以攻击 $(c, d)$，当且仅当 $a = c$ 或 $b = d$ 或 $a - b = c - d$。 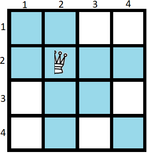 蓝色格子为被攻击的格子。 请问，最少需要放置多少枚半皇后，才能保证棋盘上的每一个格子都至少被一枚半皇后攻击？请构造一种最优方案。

第一行包含一个整数 $n$（$1 \le n \le 10^5$），表示棋盘的大小。

第一行输出一个整数 $k$，表示所需的最少半皇后数量。 接下来的 $k$ 行，每行输出两个整数 $a_i, b_i$（$1 \le a_i, b_i \le n$），表示第 $i$ 枚半皇后的位置。 如果有多种方案，输出任意一种均可。

示例 $1$：只需一枚半皇后即可。注意：在 $(1, 1)$ 放置一枚半皇后可以攻击 $(1, 1)$。 示例 $2$：同样只需一枚半皇后。在 $(1, 2)$ 或 $(2, 1)$ 放置半皇后是错误的，因为在 $(1, 2)$ 放置半皇后无法攻击 $(2, 1)$，反之亦然。在 $(2, 2)$ 放置也是一个可行的方案。 示例 $3$：无法用一枚半皇后覆盖整个棋盘。对于 $2$ 枚半皇后有多种方案，可以任选一种输出。 由 ChatGPT 4.1 翻译