CF166E Tetrahedron

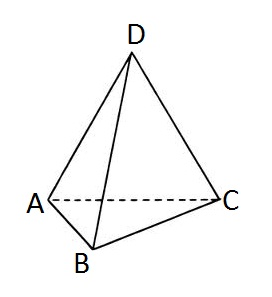
给定一个四面体，其顶点分别标记为 $A$、$B$、$C$、$D$。  一只蚂蚁站在四面体的顶点 $D$ 上。这只蚂蚁非常活跃，不能停留在原地。每次，它会沿着四面体的某条边，从一个顶点走到另一个顶点，绝不会在同一位置停留。 你的任务很简单：计算蚂蚁在恰好经过 $n$ 步后，从初始顶点 $D$ 出发回到 $D$ 的路径数量。换句话说，就是求从顶点 $D$ 出发、长为 $n$ 的不同的回路数量。由于答案可能很大，请将结果对 $1000000007$（$10^9 + 7$）取模后输出。

第一行包含唯一的正整数 $n$（$1 \leq n \leq 10^7$），表示所需回路的长度。

输出一个整数，即所需的路径数量，结果对 $1000000007$ 取模。

第一个样例中的可行路径为： - $D-A-D$ - $D-B-D$ - $D-C-D$ 由 ChatGPT 5 翻译