CF1673F Anti-Theft Road Planning
题目描述
这是一个交互题。
一座城市有 $n^2$ 栋建筑,分布在 $n$ 行 $n$ 列的网格中。你需要为每对相邻(仅通过边相邻)的建筑 $A$ 和 $B$ 之间修建一条长度为 $D(A,B)$ 的道路,长度由你选择。由于预算和法律限制,每条道路的长度必须是正整数,且所有道路的总长度不得超过 $48\,000$。
城市里有一个小偷,他会从最左上角的建筑(第一行第一列)出发,在城市中游荡,并偶尔在某些建筑中盗窃。他可以通过连接相邻建筑的道路从一栋建筑移动到另一栋相邻的建筑。
你无法追踪小偷经过了哪些建筑,也无法知道他到达这些建筑的路径。但城市中有一个追踪装置。该装置能存储一个初始为 $0$ 的整数 $x$。每当小偷通过一条长度为 $D(A,B)$ 的道路从建筑 $A$ 移动到相邻建筑 $B$ 时,追踪装置会将 $x$ 变为 $x\oplus D(A,B)$。每当小偷在某栋建筑盗窃时,追踪装置会报告当前存储的 $x$ 值,并将其重置为 $0$。
已知小偷会在恰好 $k$ 栋建筑中盗窃,但你只能在盗窃发生后获得追踪装置返回的值。你的任务是选择道路的长度,使得无论小偷采取什么策略、走什么路线,你都能仅根据追踪装置返回的值,准确判断所有被盗建筑的位置。
输入格式
首先读入一行,包含两个整数 $n$ $(2\leq n\leq 32)$ 和 $k$ $(1\leq k\leq 1024)$,分别表示行数和盗窃次数。
我们用 $B_{i,j}$ 表示第 $i$ 行第 $j$ 列的建筑。
接下来输出 $n$ 行,每行 $n-1$ 个整数,第 $i$ 行第 $j$ 个整数表示 $D(B_{i,j},B_{i,j+1})$。
再输出 $n-1$ 行,每行 $n$ 个整数,第 $i$ 行第 $j$ 个整数表示 $D(B_{i,j},B_{i+1,j})$。
注意所有道路的总长度不得超过 $48\,000$。
然后需要回答 $k$ 次询问。每次先读入追踪装置返回的值 $x$,然后输出两个整数,表示被盗建筑的行号和列号。之后才能进行下一次询问(如果还有)。
输出答案后不要忘记换行并刷新输出缓冲区,否则会收到“Idleness limit exceeded”的判罚。刷新缓冲区的方法如下:
- C++:fflush(stdout) 或 cout.flush()
- Java:System.out.flush()
- Pascal:flush(output)
- Python:stdout.flush()
- 其他语言请查阅相关文档。
Hack
本题不支持 Hack。
输出格式
见输入格式。
说明/提示
对于样例测试,$n=2$,$k=4$。
你选择如下图所示的道路长度:
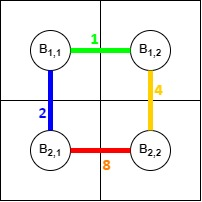
小偷采取如下策略:
1. 从 $B_{1,1}$ 出发。
2. 向右移动到 $B_{1,2}$。
3. 向下移动到 $B_{2,2}$。
4. 向左移动到 $B_{2,1}$。
5. 向上移动到 $B_{1,1}$。
6. 向右移动到 $B_{1,2}$。
7. 在 $B_{1,2}$ 盗窃。
8. 向左移动到 $B_{1,1}$。
9. 在 $B_{1,1}$ 盗窃。
10. 向下移动到 $B_{2,1}$。
11. 向右移动到 $B_{2,2}$。
12. 向上移动到 $B_{1,2}$。
13. 在 $B_{1,2}$ 盗窃。
14. 向左移动到 $B_{1,1}$。
15. 向下移动到 $B_{2,1}$。
16. 在 $B_{2,1}$ 盗窃。
追踪装置的响应如下:
1. 初始化 $x=0$。
2. $x$ 变为 $x\oplus 1=0\oplus1=1$。
3. $x$ 变为 $x\oplus 4=1\oplus4=5$。
4. $x$ 变为 $x\oplus 8=5\oplus8=13$。
5. $x$ 变为 $x\oplus 2=13\oplus2=15$。
6. $x$ 变为 $x\oplus 1=15\oplus1=14$。
7. 返回 $x=14$ 并重置 $x=0$。
8. $x$ 变为 $x\oplus 1=0\oplus1=1$。
9. 返回 $x=1$ 并重置 $x=0$。
10. $x$ 变为 $x\oplus 2=0\oplus2=2$。
11. $x$ 变为 $x\oplus 8=2\oplus8=10$。
12. $x$ 变为 $x\oplus 4=10\oplus4=14$。
13. 返回 $x=14$ 并重置 $x=0$。
14. $x$ 变为 $x\oplus 1=0\oplus1=1$。
15. $x$ 变为 $x\oplus 2=1\oplus2=3$。
16. 返回 $x=3$ 并重置 $x=0$。
由 ChatGPT 4.1 翻译