CF1675D Vertical Paths

给定一棵有 $n$ 个结点的有根树，结点编号为 $1$ 到 $n$。任意结点都可以作为树的根。 树是一个无环连通无向图。有根树是指选定一个结点作为根的树。 这棵树通过一个父节点数组 $p$ 给出，包含 $n$ 个数：$p_i$ 表示编号为 $i$ 的结点的父节点。对于结点 $u$，其父节点是从 $u$ 到根的最短路径上的下一个结点。例如，从 $5$ 到 $3$（根）的简单路径上，下一个结点是 $1$，所以 $5$ 的父节点是 $1$。 根结点没有父节点，因此对于根结点，$p_i = i$（根结点是唯一满足 $p_i = i$ 的结点）。 请找到一组路径，使得： - 每个结点恰好属于一条路径，每条路径可以包含一个或多个结点； - 在每条路径中，每个下一个结点都是当前结点的儿子（即路径总是向下——从父节点到儿子）； - 路径的数量最少。 例如，如果 $n=5$ 且 $p=[3, 1, 3, 3, 1]$，则该树可以被划分为三条路径： 1. $3 \rightarrow 1 \rightarrow 5$（包含 $3$ 个结点的路径）， 2. $4$（包含 $1$ 个结点的路径）， 3. $2$（包含 $1$ 个结点的路径）。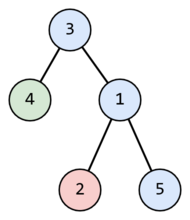  $n=5$ 时以 $3$ 为根的树划分为三条路径的示例。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例包含两行。 第一行包含一个整数 $n$（$1 \le n \le 2 \times 10^5$），表示树的结点数。 第二行包含 $n$ 个整数 $p_1, p_2, \dots, p_n$（$1 \le p_i \le n$），表示父节点数组。保证 $p$ 数组编码的是一棵有根树。 保证所有测试用例中 $n$ 的总和不超过 $2 \times 10^5$。

对于每个测试用例，第一行输出一个整数 $m$，表示最少需要多少条不相交的向下路径覆盖树的所有结点。 接下来输出 $m$ 对行，每对行描述一条路径。第一行输出该路径的长度，第二行输出该路径从上到下的结点序列。路径顺序可以任意。 如果有多种答案，输出任意一种均可。

由 ChatGPT 4.1 翻译