CF1675F Vlad and Unfinished Business

### 题意简述 有一棵 $n$ 个节点的树，从节点 $x$ 出发，需要到 $a_1,a_2\dots a_k$ 节点完成任务（任意顺序），最终到达终点 $y$。走每条边的花费为 $1$，求最小花费。

第一行一个正整数 $t$ 表示数据组数。 对于每组数据，第一行两个正整数 $n,k$ 表示节点数量和任务数量；第二行两个正整数 $x,y$ 表示起点编号和终点编号；第三行 $k$ 个正整数 $a_1,a_2\dots a_k$ 表示任务所在节点编号；接下来 $n-1$ 行，每行两个正整数表示一条边的两个端点编号。

对于每组数据，输出一行一个正整数表示最小花费。 ### 数据规模 $t\le 10^4,1\le n,k\le 2\times 10^5,\sum n\le2\times10^5$

Tree and best path for the first test case: 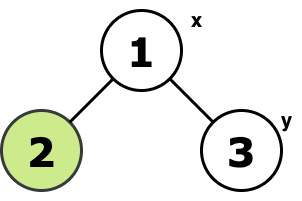 $ 1 \rightarrow 2 \rightarrow 1 \rightarrow 3 $ Tree and best path for the second test case: 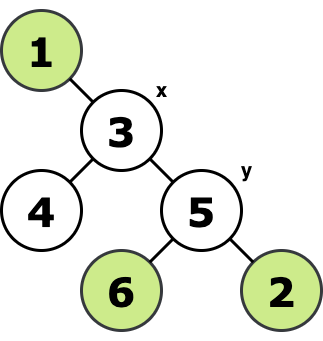 $ 3 \rightarrow 1 \rightarrow 3 \rightarrow 5 \rightarrow 2 \rightarrow 5 \rightarrow 6 \rightarrow 5 $ Tree and best path for the third test case: 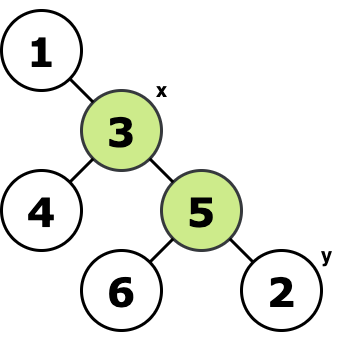 $ 3 \rightarrow 5 \rightarrow 2 $