CF1676G White-Black Balanced Subtrees

给定一棵有 $n$ 个结点的有根树，结点编号为 $1$ 到 $n$，根结点为 $1$。还有一个字符串 $s$ 表示每个结点的颜色：如果 $s_i = \texttt{B}$，则第 $i$ 个结点为黑色；如果 $s_i = \texttt{W}$，则第 $i$ 个结点为白色。 如果一棵子树中白色结点的数量等于黑色结点的数量，则称这棵子树是“平衡”的。请统计有多少棵平衡的子树。 树是一个无环连通无向图。有根树是指定了一个根结点的树，本题中所有树的根结点都是 $1$。 树通过父节点数组 $a_2, \dots, a_n$ 给出，共有 $n-1$ 个数：对于所有 $i=2,\dots,n$，$a_i$ 表示结点 $i$ 的父节点编号。结点 $u$ 的父节点是从 $u$ 到根结点的简单路径上的下一个结点。 结点 $u$ 的子树是所有在从 $u$ 到根结点的简单路径上经过 $u$ 的结点的集合。例如，下图中，$7$ 在结点 $3$ 的子树中，因为简单路径 $7 \to 5 \to 3 \to 1$ 经过了 $3$。注意，一个结点一定在它自己的子树中，根结点的子树就是整棵树。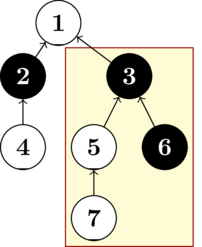  上图为 $n=7$，$a=[1,1,2,3,3,5]$，$s=\texttt{WBBWWBW}$ 的树。以结点 $3$ 为根的子树是平衡的。

输入的第一行为一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例的第一行为一个整数 $n$（$2 \le n \le 4000$），表示树的结点数。 每个测试用例的第二行为 $n-1$ 个整数 $a_2, \dots, a_n$（$1 \le a_i < i$），表示结点 $2$ 到 $n$ 的父节点编号。 每个测试用例的第三行为一个长度为 $n$ 的字符串 $s$，仅包含字符 $\texttt{B}$ 和 $\texttt{W}$，表示树的染色情况。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一个整数，表示平衡子树的数量。

第一个测试用例如题面所示。只有以结点 $2$ 和 $3$ 为根的子树是平衡的。 第二个测试用例中，只有以结点 $1$ 为根的子树是平衡的。 第三个测试用例中，只有以结点 $1$、$3$、$5$ 和 $7$ 为根的子树是平衡的。 由 ChatGPT 4.1 翻译