CF1676G White-Black Balanced Subtrees

You are given a rooted tree consisting of $ n $ vertices numbered from $ 1 $ to $ n $ . The root is vertex $ 1 $ . There is also a string $ s $ denoting the color of each vertex: if $ s_i = \texttt{B} $ , then vertex $ i $ is black, and if $ s_i = \texttt{W} $ , then vertex $ i $ is white. A subtree of the tree is called balanced if the number of white vertices equals the number of black vertices. Count the number of balanced subtrees. A tree is a connected undirected graph without cycles. A rooted tree is a tree with a selected vertex, which is called the root. In this problem, all trees have root $ 1 $ . The tree is specified by an array of parents $ a_2, \dots, a_n $ containing $ n-1 $ numbers: $ a_i $ is the parent of the vertex with the number $ i $ for all $ i = 2, \dots, n $ . The parent of a vertex $ u $ is a vertex that is the next vertex on a simple path from $ u $ to the root. The subtree of a vertex $ u $ is the set of all vertices that pass through $ u $ on a simple path to the root. For example, in the picture below, $ 7 $ is in the subtree of $ 3 $ because the simple path $ 7 \to 5 \to 3 \to 1 $ passes through $ 3 $ . Note that a vertex is included in its subtree, and the subtree of the root is the entire tree. 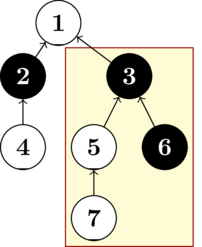 The picture shows the tree for $ n=7 $ , $ a=[1,1,2,3,3,5] $ , and $ s=\texttt{WBBWWBW} $ . The subtree at the vertex $ 3 $ is balanced.

The first line of input contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains an integer $ n $ ( $ 2 \le n \le 4000 $ ) — the number of vertices in the tree. The second line of each test case contains $ n-1 $ integers $ a_2, \dots, a_n $ ( $ 1 \le a_i < i $ ) — the parents of the vertices $ 2, \dots, n $ . The third line of each test case contains a string $ s $ of length $ n $ consisting of the characters $ \texttt{B} $ and $ \texttt{W} $ — the coloring of the tree. It is guaranteed that the sum of the values $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, output a single integer — the number of balanced subtrees.

The first test case is pictured in the statement. Only the subtrees at vertices $ 2 $ and $ 3 $ are balanced. In the second test case, only the subtree at vertex $ 1 $ is balanced. In the third test case, only the subtrees at vertices $ 1 $ , $ 3 $ , $ 5 $ , and $ 7 $ are balanced.