CF1677B Tokitsukaze and Meeting

Tokitsukaze is arranging a meeting. There are $ n $ rows and $ m $ columns of seats in the meeting hall. There are exactly $ n \cdot m $ students attending the meeting, including several naughty students and several serious students. The students are numerated from $ 1 $ to $ n\cdot m $ . The students will enter the meeting hall in order. When the $ i $ -th student enters the meeting hall, he will sit in the $ 1 $ -st column of the $ 1 $ -st row, and the students who are already seated will move back one seat. Specifically, the student sitting in the $ j $ -th ( $ 1\leq j \leq m-1 $ ) column of the $ i $ -th row will move to the $ (j+1) $ -th column of the $ i $ -th row, and the student sitting in $ m $ -th column of the $ i $ -th row will move to the $ 1 $ -st column of the $ (i+1) $ -th row. For example, there is a meeting hall with $ 2 $ rows and $ 2 $ columns of seats shown as below: There will be $ 4 $ students entering the meeting hall in order, represented as a binary string "1100", of which '0' represents naughty students and '1' represents serious students. 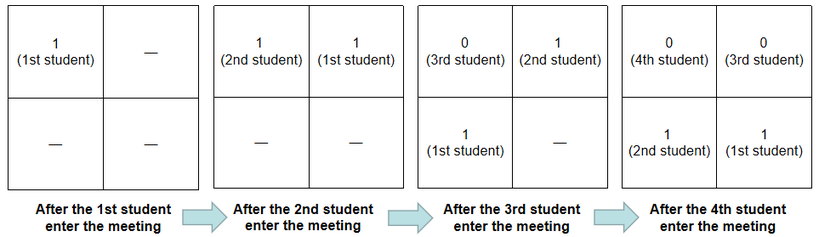The changes of seats in the meeting hall are as follows: Denote a row or a column good if and only if there is at least one serious student in this row or column. Please predict the number of good rows and columns just after the $ i $ -th student enters the meeting hall, for all $ i $ .

The first contains a single positive integer $ t $ ( $ 1 \leq t \leq 10\,000 $ ) — the number of test cases. For each test case, the first line contains two integers $ n $ , $ m $ ( $ 1 \leq n,m \leq 10^6 $ ; $ 1 \leq n \cdot m \leq 10^6 $ ), denoting there are $ n $ rows and $ m $ columns of seats in the meeting hall. The second line contains a binary string $ s $ of length $ n \cdot m $ , consisting only of zeros and ones. If $ s_i $ equal to '0' represents the $ i $ -th student is a naughty student, and $ s_i $ equal to '1' represents the $ i $ -th student is a serious student. It is guaranteed that the sum of $ n \cdot m $ over all test cases does not exceed $ 10^6 $ .

For each test case, print a single line with $ n \cdot m $ integers — the number of good rows and columns just after the $ i $ -th student enters the meeting hall.

The first test case is shown in the statement. After the $ 1 $ -st student enters the meeting hall, there are $ 2 $ good rows and columns: the $ 1 $ -st row and the $ 1 $ -st column. After the $ 2 $ -nd student enters the meeting hall, there are $ 3 $ good rows and columns: the $ 1 $ -st row, the $ 1 $ -st column and the $ 2 $ -nd column. After the $ 3 $ -rd student enters the meeting hall, the $ 4 $ rows and columns are all good. After the $ 4 $ -th student enters the meeting hall, there are $ 3 $ good rows and columns: the $ 2 $ -nd row, the $ 1 $ -st column and the $ 2 $ -nd column.